Корань (матэматыка)

| Арыфметычныя аперацыі | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
Ко́рань -й ступе́ні[1], з ліку вызначаецца як такі лік , што
Тут — так званы паказчык кораня (або ступень кораня); як правіла, ён большы або роўны 2, таму што выпадак трывіяльны.
Абазначэнне:
знак (знак кораня) у правай частцы называецца радыка́лам.
Аперацыя знаходжання кораня называецца каранява́ннем.
Лік (падкаранёвы выраз) часцей за ўсё рэчаісны або камплексны.
Прыклады для рэчаісных лікаў:
- бо
- бо
- бо
Як відаць з першага прыкладу, у рэчаіснага кораня можа быць два значэнні (дадатнае і адмоўнае), і гэта ўскладняе працу з каранямі. Каб забяспечыць адназначнасць, уводзіцца паняцце арыфметычнага кораня, значэнне якога заўсёды неадмоўнае, у першым прыкладзе гэта лік 3.
Азначэнне і звязаныя паняцці[правіць | правіць зыходнік]
Акрамя прыведзенага вышэй, можна даць два раўнасільныя азначэнні кораня[2]:
- Корань -й ступені з ліку ёсць рашэнне ураўнення (адзначым, што рашэнняў можа быць некалькі або ні аднаго).
- Корань -й ступені з ліку ёсць корань мнагачлена гэта значыць значэнне , пры якім гэты мнагачлен роўны нулю.

Аперацыя вылічэння называецца «здабываннем кораня -й ступені» з ліку . Гэта адна з двух аперацый, адваротных да ўзвядзення ў ступень[3], а іменна — знаходжанне асновы ступені па вядомым паказчыку і выніку ўзвядзення ў ступень . Другая адваротная аперацыя, лагарыфмаванне, знаходзіць паказчык ступені па вядомых аснове і выніку.
Карані другой і трэцяй ступені ўжываюцца асабліва часта і таму маюць спецыяльныя назвы[3].
- Квадратны корань: У гэтым выпадку паказчык ступені 2 звычайна апускаецца, а тэрмін «корань» без ўказання ступені часцей за ўсё абазначае квадратны корань.
- Кубічны корань:
Карані з рэчаісных лікаў[правіць | правіць зыходнік]
Корань -й ступені з рэчаіснага ліку , у залежнасці ад цотнасці і знака , можа мець ад 0 да 2 рэчаісных значэнняў.
Агульныя ўласцівасці[правіць | правіць зыходнік]
- Корань няцотнай ступені з дадатнага ліку — дадатны лік, адназначна вызначаны.
| , дзе — няцотны |
- Напрыклад,
- Корань няцотнай ступені з адмоўнага ліку — адмоўны лік, адназначна вызначаны.
| , дзе — няцотны |
- Напрыклад,
- Корань цотнай ступені з дадатнага ліку мае два значэнні, роўныя па модулю, але з процілеглымі знакамі.
| , дзе — цотны |
- Напрыклад,
- Корань цотнай ступені з адмоўнага ліку не існуе ў вобласці рэчаісных лікаў, бо пры ўзвядзенні любога рэчаіснага ліку ў ступень з цотным паказчыкам вынікам будзе неадмоўны лік. Ніжэй будзе паказана, як здабываць такія карані ў шырэйшай сістэме — мностве камплексных лікаў (тады значэннямі кораня будуць камплексных лікаў).
| не існуе, калі — цотны |
- Корань любой натуральнай ступені з нуля — нуль.
| дзе |

Арыфметычны корань[правіць | правіць зыходнік]
Карані цотнай ступені вызначаны, наогул кажучы, неадназначна, гэта стварае нязручнасці пры іх выкарыстанні. Таму з практычных меркаванняў было ўведзена абмежаванне гэтага паняцця[4].
Арыфметычны корань -й ступені з неадмоўнага рэчаіснага ліку — гэта такі неадмоўны лік , што
Абазначаецца арыфметычны корань тым жа знакам радыкала.
Такім чынам, арыфметычны корань, у адрозненне ад раней вызначанага (алгебраічнага[5]), вызначаецца толькі для неадмоўных рэчаісных лікаў, а яго значэнне заўсёды існуе, неадмоўнае і адназначна вызначана[6]. Напрыклад, квадратны корань з ліку 4 мае два значэнні: 2 і -2, з іх арыфметычным з'яўляецца першае.
- Арыфметычны корань і алгебраічны абазначаюцца адным і тым жа сімвалам, але з'яўляюцца рознымі аб'ектамі, таму ў рамках дадзенага артыкула арыфметычны корань абазначаецца сінім колерам, а алгебраічны — чорным.
Алгебраічныя ўласцівасці[правіць | правіць зыходнік]
Прыведзеныя ніжэй формулы верныя, перш за ўсё, для арыфметычных каранёў любой ступені, што падкрэсліваецца вылучэннем знака радыкала сінім колерам (акрамя асобна абумоўленых выпадкаў). Яны справядлівыя таксама для каранёў няцотнай ступені, у якіх дапускаюцца і адмоўныя падкаранёвыя выразы[7].
- Узаемапагашэнне кораня і ступені[8]
- для няцотнага :
- для цотнага :
- Калі , то і
- Корань са здабытку роўны здабытку каранёў з сумножнікаў:
- Корань з дзелі роўны дзелі каранёў:
- Наступная роўнасць вызначае ўзвядзенне ў дробную (рацыянальную) ступень[9]:
- Велічыня кораня не зменіцца, калі яго паказчык і ступень падкаранёвага выразу падзяліць на іх агульны множнік:
- Прыклад:
- Пры здабыванні кораня з кораня іх паказчыкі перамнажаюцца (г. зн. выніковы корань мае паказчык, роўны здабытку паказчыкаў каранёў):
- Для каранёў няцотнай ступені знак мінуса можна выносіць з-пад кораня:
Здабыванне кораня і ўзвядзенне ў дробную ступень[правіць | правіць зыходнік]
Аперацыя ўзвядзення ў ступень першапачаткова была ўведзена як скарочаны запіс аперацыі множання натуральных лікаў:
- (n разоў).
Наступным крокам было вызначэнне ўзвядзення ў адвольную цэлую, у тым ліку адмоўную, ступень:
Аперацыя здабывання арыфметычнага кораня дазваляе вызначыць узвядзенне дадатнага ліку ў любую рацыянальную (дробную) ступень[9]:
Пры гэтым лічнік дробу можа мець знак. Уласцівасці пашыранай аперацыі ў асноўным такія ж, як і ва ўзвядзення ў цэлую ступень.
Такое вызначэнне азначае, што здабыванне кораня і адваротнае да яго узвядзенне ў ступень па сутнасці аб'ядноўваюцца ў адну алгебраічную аперацыю. У прыватнасці:
Спробы ўзвядзення ў рацыянальную ступень адмоўных лікаў могуць прывесці да памылак, бо значэнне алгебраічнага кораня вызначана неадназначна, а вобласць значэнняў арыфметычнага кораня абмежавана неадмоўными лікамі. Прыклад магчымай памылкі:
Функцыя кораня[правіць | правіць зыходнік]
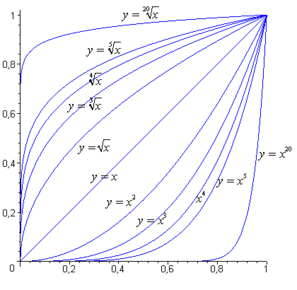
- Графікі функцый кораня
-
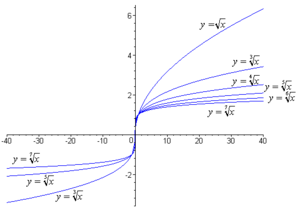
Функцыі кораня і адваротныя да іх ступенныя функцыі на прамежку
-
Функцыі кораня:
— арыфметычны, цотныя ступені 2, 4, 6
— агульны, няцотныя ступені 3, 5, 7
Калі разглядаць падкаранёвы выраз як зменную, мы атрымаем функцыю кораня -й ступені:
Функцыя кораня адносіцца да катэгорыі алгебраічных функцый. Графік любой функцыі кораня праходзіць праз пачатак каардынат і кропку .
Як сказана вышэй, для кораня цотнай ступені, каб забяспечыць адназначнасць функцыі, корань павінен быць арыфметычным, так што аргумент неадмоўны. Функцыя кораня няцотнай ступені адназначная і існуе для любога рэчаіснага значэння аргумента.
| Тып функцыі кораня | Вобласць вызначэння | Вобласць значэнняў | Іншыя ўласцівасці |
|---|---|---|---|
| Цотнай ступені | Функцыя выпуклая ўверх на ўсей вобласці вызначэння | ||
| Няцотнай ступені | Функцыя няцотная |
Для любой ступені функцыя кораня строга ўзрастае, непарыўная ўсюды ўнутры сваёй вобласці вызначэння. Неабмежавана дыферэнцавальная ўсюды, акрамя пачатку каардынат, дзе вытворная становіцца бесканечнаю[10][11]. Вытворная вызначаецца па формуле[12]:
У прыватнасці,
Функцыя неабмежавана інтэгравальная ва ўсёй вобласці вызначэння. Нявызначаны інтэграл атрымліваецца па формуле:
У прыватнасці,
дзе — адвольная пастаянная.
Гранічныя суадносіны[правіць | правіць зыходнік]
Прывядзём некалькі карысных граніц, якія змяшчаюць карані[15]:
Практычнае вылічэнне каранёў[правіць | правіць зыходнік]
Квадратныя і кубічныя карані звычайна прадугледжаны ва ўсіх калькулятарах. Для ступеней, вышэйшых за трэцюю, можна выкарыстоўваць лагарыфмічную тоеснасць:
З яе вынікае, што для здабывання кораня трэба знайсці лагарыфм падкарэннага выразу, падзяліць на ступень кораня і знайсці антылагарыфм выніку.
Карані з камплексных лікаў[правіць | правіць зыходнік]
Гістарычна паняцце камплекснага ліку ўзнікла ў сувязі з жаданнем "узаконіць" квадратныя карані з адмоўных лікаў. Як паступова высветлілася, камплексныя лікі маюць багатыя алгебраічныя і аналітычнымі ўласцівасці; у прыватнасці, здабыванне каранёў з іх заўсёды магчыма, хоць і неадназначна.
Спосабы знаходжання[правіць | правіць зыходнік]
Запішам камплексны лік ў трыганаметрычнай форме:
Тады карані -й ступені з вызначаюцца формулай Муаўра (трыганаметрычная форма)[16]:

або ў паказчыкавай форме:
|
Абазначэнні
|
Корань ступені з ненулявога камплекснага ліку мае значэнняў (гэта вынік асноўнай тэарэмы алгебры), і ўсе яны розныя. Значэнне кораня, якое атрымліваецца пры , часта называецца галоўным.
Для ўсіх значэнняў кораня велічыня модуля аднолькавая (ён вызначаецца як арыфметычны корань з модуля першапачатковага камплекснага ліку), а змяняецца толькі яго аргумент, таму ўсе значэнняў кораня размяшчаюцца на камплекснай плоскасці на акружнасці радыуса з цэнтрам у пачатку каардынат. Карані дзеляць гэтую акружнасць на роўных частак.
Прыклады[правіць | правіць зыходнік]
Знойдзем . Маем
Адкуль па формуле атрымліваем:
Пры атрымаем першы корань , пры атрымаем другі корань
Далей знойдзем . З тоеснасці
па формуле атрымліваем два карані:
Камплексная функцыя кораня і рыманава паверхня[правіць | правіць зыходнік]
Разгледзім камплексную функцыю кораня n-й ступені:
Паводле сказанага вышэй, гэтая функцыя з'яўляецца шматзначнай (дакладней, n-значнай) функцыяй, і гэта стварае нязручнасці пры яе даследаванні і ўжыванні. У камплексным аналізе замест разгляду мнагазначных функцый на камплекснай плоскасці прынята іншае рашэнне: разглядаць функцыю як адназначную, але вызначаную не на плоскасці, а на больш складанай мнагастайнасці, якая называецца рыманавай паверхняй[17].
-
Рыманава паверхня для камплекснага квадратнага кораня
-
Рыманава паверхня для камплекснага кораня 4-й ступені
Для камплекснай функцыі кораня n-й ступені яе рыманава паверхня (гл. малюнкі) складаецца з n абласцей (лістоў), звязаных шрубападобна, прычым апошні ліст звязаны з першым. Гэта паверхня непарыўная і адназвязная. Адзін з лістоў утрымлівае галоўныя значэнні кораня, якія атрымліваюцца як аналітычны працяг рэчаіснага кораня з дадатнага прамяня рэчаіснай восі.
Апішам дзеля прастаты камплексную функцыю квадратнага кораня. Яе рыманава паверхня складаецца з двух лістоў. Першы ліст можна прадставіць як комплексную плоскасць, у якой выразаны дадатны прамень рэчаіснай восі. Значэнні функцыі кораня на гэтым лісце маюць удвая меншы аргумент, чым , і таму яны запаўняюць верхнюю частку камплекснай плоскасці значэнняў. На разрэзе першы ліст злеплены з другім, і функцыя непарыўна працягваецца праз разрэз на другі ліст, дзе яе значэнні запаўняюць ніжнюю частку камплекснай плоскасці значэнняў. Пачатак першага ліста і канец другога, што засталіся свабоднымі, таксама склеім, пасля чаго атрыманая функцыя на рыманавай паверхні становіцца адназначнай і ўсюды непарыўнай[17].
Функцыя мае адзін нуль пры . Асаблівыя кропкі: і (кропкі разгалінавання бясконцага парадку)[17]. Наяўнасць пункта разгалінавання ў нулі азначае, што любы замкнёны контур, які ахоплівае нуль, непазбежна пераходзіць з ліста на ліст.
Дзякуючы адназвязнасці рыманава паверхня кораня з'яўляецца ўніверсальнай накрываючай[18] для камплекснай плоскасці без пункта .
Варыяцыі і абагульненні[правіць | правіць зыходнік]
Корань -й ступені з ёсць рашэнне ўраўнення
і яго ў прынцыпе можна вызначыць ўсюды, дзе такое ўраўненне мае сэнс. Часцей за ўсё разглядаюць такія абагульненні ў алгебраічных колцах. Лепш за ўсё даследаваны абагульненыя квадратныя карані.
Калі колца ёсць вобласць цэласнасці, то квадратных каранёў можа быць альбо два, альбо ні аднаго. На самай справе, калі маюцца два кораня то
адкуль:
а раз дзельнікаў нуля няма, то
У больш агульным выпадку, калі ў колцы ёсць дзельнікі нуля ці яно некамутатыўнае (мае неперастаўляльную аперацыю множання), лік каранёў можа быць любым.
Карані для кватэрніёнаў маюць шмат агульнага з камплекснымі, але ёсць і істотныя асаблівасці. Квадратны кватэрніённы корань звычайна мае 2 значэнні, але калі падкаранёвы выраз — адмоўны рэчаісны лік, то значэнняў бясконца шмат. Напрыклад, квадратныя карані з ўтвараюць трохмерную сферу, якая вызначаецца формулай[19]:
Для колца квадратных матрыц даказана, што калі матрыца дадатна вызначана, то дадатна вызначаны квадратны корань з яе існуе і адзіны[20]. Для матрыц іншых тыпаў каранёў можа колькі заўгодна (у тым ліку ні аднаго).
Квадратныя карані ўводзяцца таксама для функцый[21], аператараў[22] і іншых матэматычных аб'ектаў.
Гісторыя[правіць | правіць зыходнік]
Развіццё паняцця[правіць | правіць зыходнік]

Першыя задачы, звязаныя са здабываннем квадратнага кораня, знойдзены ў працах вавілонскіх матэматыкаў (пра дасягненні старажытнага Егіпта ў гэтых задачах нічога не вядома). Сярод такіх задач[23]:
- Прымяненне тэарэмы Піфагора для знаходжання стараны прамавугольнага трохвугольніка па вядомых двух іншых старанах.
- Знаходжанне стараны квадрата, плошча якога зададзена.
- Рашэнне квадратных ураўненняў.
Вавілонскія матэматыкі (II тысячагоддзе да н. э.) распрацавалі для здабывання квадратнага кораня асаблівы лікавы метад. Пачатковае прыбліжэнне для разлічваліся зыходзячы з найбліжэйшага да кораня (у меншы бок) натуральнага ліку . Прадставіўшы падкаранёвы выраз у выглядзе:
атрымліваем:
затым прымяняўся ітэратыўны працэс ўдакладнення, адпаведны метаду Ньютана[24]:
Ітэрацыі ў гэтым метадзе вельмі хутка сыходзяцца. Для , напрыклад, і мы атрымліваем паслядоўнасць прыбліжэнняў:
У апошнім значэнні верныя ўсе лічбы, акрамя апошняй.
Аналагічныя задачы і метады сустракаюцца ў старажытнакітайскай «Матэматыцы ў дзевяці кнігах»[25]. Старажытныя грэкі зрабілі важнае адкрыццё: — ірацыянальны лік. Дэталёвае даследаванне, выкананае Тээтэтам Афінскім (IV стагоддзе да н. э.), паказала, што калі корань з натуральнага ліку не здабываецца цалкам, то яго значэнне ірацыянальнае[26].
Грэкі сфармулявалі праблему падваення куба, якая зводзілася да пабудовы кубічнага кораня з дапамогай цыркуля і лінейкі. Праблема аказалася невырашальнай. Лікавыя алгарытмы здабывання кубічнага кораня апублікавалі Герон (у трактаце "Метрыка", I стагоддзе н. э.) і індыйскі матэматык Арыябхата I (V стагоддзе)[27]. Алгарытмы здабывання каранёў любой ступені з цэлага ліку, распрацаваныя індыйскімі і ісламскімі матэматыкамі, былі ўдасканалены ў сярэднявечнай Еўропе. Мікалай Арэм (XIV стагоддзе) упершыню растлумачыў[28] корань -й ступені як узвядзенне ў ступень
Пасля з'яўлення формулы Кардана (XVI стагоддзе) пачалося прымяненне ў матэматыцы ўяўных лікаў, якія разумеюцца як квадратныя карані з адмоўных лікаў[29]. Асноўныя прыёмы вылічэнняў з камплекснымі лікамі распрацаваў у XVI стагоддзі Рафаэль Бамбелі, які таксама прапанаваў арыгінальны метад вылічэння каранёў (з дапамогай ланцуговых дробаў). Адкрыццё формулы Муаўра (1707) паказала, што здабыванне кораня любой ступені з камплекснага ліку заўсёды магчыма і не прыводзіць да новага тыпу лікаў[30].
Камплексныя карані адвольнай ступені ў пачатку XIX стагоддзя глыбока даследаваў Гаус, хоць першыя вынікі належаць Эйлеру[31]. Надзвычай важным адкрыццём (Галуа) стаў доказ таго факта, што не ўсе алгебраічныя лікі (карані мнагачлена) можна атрымаць з натуральных з дапамогай чатырох дзеянняў арыфметыкі і здабывання кораня[32].
Этымалогія тэрміна і паходжанне сімволікі[правіць | правіць зыходнік]
Тэрмін корань мае доўгую і складаную гісторыю. Здабыванне квадратнага кораня старажытныя грэкі разумелі строга геаметрычна: як знаходжанне стараны квадрата па вядомай яго плошчы. Пасля перакладу на санскрыт грэчаскае слова "старана" ператварылася ў «мула» (аснова). Слова «мула» мела таксама значэнне «корань», таму пры перакладзе індыйскіх сідхант на арабскую мову выкарыстоўваўся тэрмін «джызр» (корань расліны). Пасля аналагічнае па сэнсе слова «radix» замацавалася ў лацінскіх перакладах з арабскай, а праз іх і ў славянскіх матэматычных тэрміналогіях («корань», «радыкал»)[33].
Сярэднявечныя матэматыкі (напрыклад, Кардана) абазначалі квадратны корань[34] сімвалам Rx, скарачэнне ад слова «radix». Сучаснае абазначэнне упершыню ўжыў нямецкі матэматык Крыстаф Рудольф, са школы касістаў (гэта значыць алгебраістаў), у 1525[35]. Паходзіць гэты знак ад стылізаванай першай літары таго ж слова «radix». Лінія над падкаранёвым выразам спачатку адсутнічала; яе пазней увёў Дэкарт (1637) для іншай мэты (замест дужак), і гэтая рыса неўзабаве злілася са знакам кораня.
Паказчык ступені з'явіўся ў знаку кораня дзякуючы Валісу і «Універсальнай арыфметыцы» Ньютан (XVIII стагоддзе)[36].
Гл. таксама[правіць | правіць зыходнік]
Зноскі
- ↑ Корань // Матэматычная энцыклапедыя / Гал. рэд. В.Бернік. — Мінск: Тэхналогія, 2001. — С. 171.
- ↑ М. И. Сканави. Элементарная математика. п.1.11, стр.49.
- ↑ а б Выгодский М. Я. Справочник по элементарной математике 1978, с. 64..
- ↑ Арифметический корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.
- ↑ Алгебраічны (шматзначны) корань у крыніцах часта называюць проста коранем.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления 1966, Т. I, С. 35—36..
- ↑ Выгодский М. Я. Справочник по элементарной математике 1978, с. 141—143..
- ↑ Алгебра и начала анализа. Учебник для 10—11 классов, под ред. А. Н. Колмогорова. М.: Просвещение, 2002, С. 209.
- ↑ а б Выгодский М. Я. Справочник по элементарной математике 1978, с. 183..
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления 1966, Т. I, С. 194, 198..
- ↑ Мордкович А. Г. 2003, с. 236—238..
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления 1966, Т. I, С. 215..
- [[#cite_ref-FOOTNOTEФихтенгольц_Г._М._Курс_дифференциального_и_интегрального_исчисления1966Т._I,_С._233,_асобны_выпадак_для_'"`UNIQ--math-00000083-QINU`"'_13-0|↑]] Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления 1966, Т. I, С. 233, асобны выпадак для .
- ↑ Не блытаць з кратнымі інтэграламі. Іх запісы вельмі падобныя, але -ы інтэграл з'яўляецца нявызначаным, у той час як -кратны інтэграл — вызначаны.
- ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления 1966, Том I, стр. 67, 131—132, 164, 166—167..
- ↑ Корн Г., Корн Т. Справочник по математике 1973, с. 36—37..
- ↑ а б в Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной 1967, с. 96-99, 28—29..
- ↑ Болтянский В. Г., Ефремович В. А. Наглядная топология. — М.: Наука, 1982. — С. 112. — (Библиотечка Квант, выпуск 21).
- ↑ Porteous, Ian R. Clifford Algebras and the Classical Groups. Cambridge, 1995, page 60.
- ↑ Гл., напрыклад: Гантмахер Ф. Р.. Теория матриц. М.: ГИТТЛ, 1953, С. 212—219, або: Воеводин В., Воеводин В. Энциклопедия линейной алгебры. Электронная система ЛИНЕАЛ. Спб.: БХВ-Петербург, 2006.
- ↑ Гл., напрыклад: Ершов Л. В., Райхмист Р. Б. Построение графиков функций. М.: Просвещение, 1984, або Каплан И. А. Практические занятия по высшей математике. Харьков: Изд-во ХГУ, 1966.
- ↑ Гл., напрыклад: Хатсон В., Пим Дж. Приложения функционального анализа и теории операторов. М.: Мир, 1983, або: Халмош П. Гильбертово пространство в задачах. М.: Мир, 1970.
- ↑ История математики 1970—1972, Том I, С. 42—46..
- ↑ История математики 1970—1972, Том I, С. 47..
- ↑ История математики 1970—1972, Том I, С. 169—171..
- ↑ Башмакова И. Г. Становление алгебры (из истории математических идей). — М.: Знание, 1979. — С. 23.. — (Новое в жизни, науке, технике. Математика, кибернетика, № 9).
- ↑ Abhishek Parakh. Ariabhata's root extraction methods // Indian Journal of History of Science. — 2007. — В. 42.2. — С. 149—161. Архівавана з першакрыніцы 9 чэрвеня 2010.
- ↑ История математики 1970—1972, Том I, С. 275—276..
- ↑ История математики 1970—1972, Том I, С. 296—298..
- ↑ История математики 1970—1972, Том III, С. 56—59..
- ↑ История математики 1970—1972, Том III, С. 62..
- ↑ Колмогоров А. Н., Юшкевич А. П. (ред.). Математика XIX века. Математическая логика, алгебра, теория чисел, теория вероятностей. — М.: Наука, 1978. — Т. I. — С. 58—66..
- ↑ История математики 1970—1972, Том I, С. 185..
- ↑ Никифоровский В. А. Из истории алгебры XVI-XVII вв. — М.: Наука, 1979. — С. 81. — 208 с. — (История науки и техники).
- ↑ Знаки математические // Математическая энциклопедия. — М.: Советская Энциклопедия, 1982. — Т. 2.
- ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб.: ЛКИ, 2008. — С. 82. — 248 с. — ISBN 978-5-382-00839-4.
Літаратура[правіць | правіць зыходнік]
- Выгодский М. Я. Справочник по элементарной математике. — изд. 25-е. — М.: Наука, 1978. — ISBN 5-17-009554-6.
- История математики, в трёх томах / Под редакцией А. П. Юшкевича. — М.: Наука, 1970—1972.
- Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с.
- Мордкович А. Г. Алгебра и начала анализа. Учебник для 10—11 классов, часть 1. — изд. 4-е. — М.: Мнемозина, 2003. — 376 с.
- Свешников А. Г., Тихонов А. Н. Теория функций комплексной переменной. — М.: Наука, 1967. — 304 с.
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — 680 с.
- Корень // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 3.
Гэты артыкул уваходзіць у лік добрых артыкулаў беларускамоўнага раздзела Вікіпедыі. |











![{\displaystyle \scriptstyle {\sqrt[{\text{паказчык}}]{\scriptstyle {\text{падкаранёвы выраз}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c32f318a7a54a6b0726409a345eb29cee68b1bf)









![{\displaystyle b={\sqrt[{n}]{a}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faa9d021810625038d355d8d04e49225a5f25121)
![{\displaystyle {\sqrt[{2}]{9}}=\pm 3,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c6c68e659a7a99332be1cfa67dd7c2ad9ebb9af3)

![{\displaystyle {\sqrt[{3}]{\ 64}}=4,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/20c4beeb304fe77e586206e908c1ee4f7b6f267c)

![{\displaystyle {\sqrt[{3}]{\frac {8}{27}}}={\frac {2}{3}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bdc22590a600d2eedc6841477696f1ae07ed9a)




![{\displaystyle {\sqrt[{n}]{a}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7873203eb76042fcd24056c553de8c86054a2df)


![{\displaystyle {\sqrt[{3}]{a}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0a8092bee1ed820e5f8f1d7a2d8696c53a55fea7)
![{\displaystyle {\sqrt[{n}]{a}}=b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a689688935f6bb305cb30a3f4d178cc01d49bb9)

![{\displaystyle {\sqrt[{3}]{125}}=5,\ {\sqrt[{5}]{32}}=2,\ {\sqrt[{15}]{1}}=1,\ 36-{\sqrt[{3}]{1336-5}}=36-{\sqrt[{3}]{1331}}=36-11=25}](https://wikimedia.org/api/rest_v1/media/math/render/svg/138eacc9134cf93dfffcbcbc7c96b355678c0bec)

![{\displaystyle {\sqrt[{3}]{-8}}=-2,\ {\sqrt[{5}]{-243}}=-3,\ {\sqrt[{7}]{-1}}=-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e37b2821a200bbf758c4661d5b13ee407a3d2f9)
![{\displaystyle {\sqrt[{n}]{a}}=\pm b}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bf21563d513e7b8292a2e4eea8618aa3bbfcfbc9)
![{\displaystyle {\sqrt {36-11}}={\sqrt {25}}=\pm 5,\ \ {\sqrt[{4}]{81}}=\pm 3,\ \ {\sqrt[{10}]{1024}}=\pm 2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6028eedbf969328ee0bf9f1577f0577b483c2ae6)

![{\displaystyle {\sqrt[{n}]{0}}=0,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c650afa98b96756d746750fcaac8f71275a749a5)

![{\displaystyle ~{\sqrt[{n}]{a^{n}}}=a,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca68744ed716ced7bbab001821c4cebb6807c13c)
![{\displaystyle ~{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{n}}}}}=|a|.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cbecaa958da5eb4b9e62f3087ee514fb994ed2d8)

![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}<{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd8a577e4f3d79fce7791fe7b6242a87c959c07a)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{ab}}}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab4f987edd67897546b66a0aa8ce41595459a135)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{\frac {a}{b}}}}}={\frac {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{b}}}}},\;b\neq 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3710335cb407ed4643e06a4971fea8d03f50837a)
![{\displaystyle a^{m/n}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}}=\left({\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}\right)^{m}=\left(a^{1/n}\right)^{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/37615b317944b42c53b5de05431bc3369c3f59af)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}nk}]{\color {black}{a^{mk}}}}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}},\;n,k\in \mathbb {N} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf6d3911501828794dae6ce86de52f73bcf0e394)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}6}]{\color {black}{64}}}}={\color {blue}{\sqrt[{\color {black}{2\cdot 3}}]{\color {black}{4^{3}}}}}={\color {blue}{\sqrt {\color {black}{4}}}}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c63d5e94e829da11f858861200e5fcada0281e5b)
![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {blue}{\sqrt[{\color {black}k}]{\color {black}{a}}}}}}={\color {blue}{\sqrt[{\color {black}nk}]{\color {black}{a}}}},\quad n,k\in \mathbb {N} .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5e92fd6d0fdc29580ebec764868b4dc12be697c)
![{\displaystyle {\sqrt[{n}]{-a}}=-{\sqrt[{n}]{a}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af6690b53718feb4a293f7d64dc4f657e32664b8)


![{\displaystyle a^{\frac {m}{n}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a^{m}}}}},\quad a>0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66c990f0d36264e0e45b5f6c774ca113b25f62cd)


![{\displaystyle ~{\color {blue}{\sqrt[{\color {black}n}]{\color {black}{a}}}}=a^{\frac {1}{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0306ec45eaed50f4a8012016c6acd7a0b3268ff9)

![{\displaystyle [0;\ 1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bd9d07c3fa150a68ff70c59f5360476fd970cdc)
![{\displaystyle y={\sqrt[{n}]{x}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83b223891796710c0bba8ef12c07efb061b8e3b6)



![{\displaystyle {\frac {d}{dx}}{\sqrt[{n}]{x}}={\frac {1}{n{\sqrt[{n}]{x^{n-1}}}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9cf2d55214c475a0f33bb134acc8d4e8cc75c5a0)

![{\displaystyle \int {\sqrt[{n}]{x}}\;dx={\frac {\sqrt[{n}]{x^{n+1}}}{1+{\frac {1}{n}}}}+C.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/70cea7a23cb182eab6b216d5995332883c4e78f6)



![{\displaystyle {\sqrt[{n}]{x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b3ba2638d05cd9ed8dafae7e34986399e48ea99)
![{\displaystyle {\frac {d^{k}}{dx^{k}}}{\sqrt[{n}]{x}}=(-1)^{k}{\frac {\prod _{m=0}^{k-1}(mn-1)}{{n^{k}}{\sqrt[{n}]{x^{kn-1}}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6f3373038a13a0c053735d14061dfb06a12c19)

![{\displaystyle \underbrace {\int \cdots \int } _{k}{\sqrt[{n}]{x}}\,\underbrace {dx\cdots dx} _{k}={\frac {{n^{k}}{\sqrt[{n}]{x^{kn+1}}}}{\prod _{m=1}^{k}(1+mn)}}+C,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51ad83c9f909d4382bc8fa0e4f73c698c91f126e)

![{\displaystyle \lim _{n\to \infty }{\sqrt[{n}]{n}}=\lim _{n\to \infty }{\sqrt[{n}]{\ln n}}=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f0e1e5e54014face5332313d4e1aefc3e6860fb)
![{\displaystyle \lim _{n\to \infty }n\left({\sqrt[{n}]{x}}-1\right)=\lim _{n\to \infty }n\left(1-{\frac {1}{\sqrt[{n}]{x}}}\right)=\ln x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/83d95e2439ebe22e00bd6addcf35e3377c462c23)
![{\displaystyle \lim _{x\to 0}{\frac {{\sqrt[{n}]{(x+1)^{m}}}-1}{x}}={\frac {m}{n}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d69c07700c69c3c6ea11288bea5bc3b878ae7fc)
![{\displaystyle \lim _{n\to \infty }\left({\frac {{\sqrt[{n}]{a}}+{\sqrt[{n}]{b}}}{2}}\right)^{n}={\sqrt {ab}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59682d9b7c62b477d266fd422777cc3a7235143f)
![{\displaystyle \log _{a}{\sqrt[{n}]{x}}={\frac {\log _{a}(x)}{n}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/951ecbd8250645112d30464ccdb54f27e55fc22b)


![{\displaystyle {\sqrt[{n}]{z}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}\left(\cos {\frac {\varphi +2\pi k}{n}}+i\sin {\frac {\varphi +2\pi k}{n}}\right),\;k=0,1,\dots ,n-1,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4bccd694bd9c17756b8748558e5de056650960d8)

![{\displaystyle {\sqrt[{n}]{z}}={\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}e^{\left(i{\frac {\varphi +2\pi k}{n}}\right)},\;k=0,1,\dots ,n-1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2f6d3be5a62a188a60a4a4145180074800bc2a3f)








![{\displaystyle {\color {blue}{\sqrt[{\color {black}n}]{\color {black}{r}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d735d37172f368d019ceb8f67b7cd38a5982c58a)









![{\displaystyle w={\sqrt[{n}]{z}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fe2a25829482fe1c9b8dd10f629067ba547992af)
























