Ступеняванне
| Арыфметычныя аперацыі | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
Узвядзе́нне ў ступе́нь (ці падвышэ́нне да ступе́ні[1]), або ступеняванне[1] — арыфметычная аперацыя над двума лікамі: асновай b і пака́зчыкам (або ступе́нню) n. На пісьме ступеняванне пазначаецца як bn. Калі n ёсць натуральным лікам, ступеняванне адпавядае кратнаму (паўтаральнаму) множанню; інакш кажучы, b ў ступені n — гэта здабытак n множнікаў, кожны з якіх роўны b (такі здабытак таксама называецца ступенню):
Тут відаць падабенства з аперацыяй множання на натуральны лік, якая адпавядае кратнаму складанню:
Гістарычна, аперацыя ступенявання была спачатку вызначана для натуральных лікаў, і толькі потым, з цягам часу, яна была распаўсюджана на адмоўныя цэлыя ступені (увабраўшы ў сябе аперацыю кратнага дзялення), на рацыянальныя ступені (такім чынам, сюды была ўключана і аперацыя здабывання кораня). Пазней ступеняванне для адвольных рэчаісных ступеней было вызначана як непарыўны працяг з мноства рацыянальных ступеней.
Паказчык ступені звычайна запісваюць як надрадковы знак справа ад асновы. Запіс ступенявання bn можна чытаць наступным чынам:
- b ўзве́дзенае ў n-ую ступе́нь,
- b ўзве́дзенае ў ступе́нь n ,
- b ў ступе́ні n ,
- або коратка, b ў n-ай.
Некаторыя ступені маюць свае ўласныя назвы:
- b² звычайна называюць квадра́там ліку b і чытаюць як b ў квадраце,
- b³ называецца ку́бам ліку b і чытаюць як b ў кубе.
Таксама варта падкрэсліць некаторую розніцу паміж тэрмінамі «ўзвядзенне ў ступень» і «ступеняванне»:
- словазлучэнне «ўзвядзенне ў ступень» ужываецца, калі паказчык ступені — сталая велічыня, а аснова — зменная.
- слова «ступеняванне» выкарыстоўваюць, калі маюць на ўвазе, што паказчык з'яўляецца зменнай велічынёй, а аснова нязменная.
Аднак у якасці назвы аперацыі і ў выпадках, калі не трэба падкрэсліваць сталасць ці зменнасць аргументаў, аднолькава можна ўжываць і «ступеняванне», і «ўзвядзенне ў ступень».
Як адзначалася вышэй, ступень bn можна вызначыць і для адмоўных цэлых n, калі b не нуль. Не існуе натуральнага пашырэння ступенявання на ўсе рэчаісныя асновы b і паказчыкі n, аднак калі аснова b з'яўляецца дадатным рэчаісным лікам, ступеняванне bn можна вызначыць для ўсіх рэчаісных і нават камплексных паказчыкаў n з дапамогай паказнікавай функцыі ez. Трыганаметрычныя функцыі таксама можна выразіць праз камплекснае ступеняванне.
Ступеняванне матрыц выкарыстоўваецца пры развязанні сістэм лінейных дыферэнцыяльных ураўненняў.
Ступеняванне паўсюдна сустракаецца ў шматлікіх мадэлях і вылічэннях у самых разнастайных галінах навукі і прамысловасці, сюды можна ўключыць фізіку (хвалі, ядзерны распад), хімію (хімічная кінетыка), біялогію (рост папуляцый), эканоміку (складаныя працэнты) і камп'ютарныя навукі (крыптаграфія з адкрытым ключом).

Цэлыя паказчыкі[правіць | правіць зыходнік]
Для ступенявання з цэлымі паказчыкамі патрэбна толькі элементарная алгебра.
Натуральныя паказчыкі[правіць | правіць зыходнік]
Фармальнае азначэнне:
Ступені з натуральным паказчыкам можна вызначыць з дапамогай пачатковай умовы
- .
Са спалучальнасці множання вынікае, што для любых натуральных m і n,
Адвольныя цэлыя паказчыкі[правіць | правіць зыходнік]
Пры ненулявых b і натуральных n зваротныя суадносіны з папярэдняга падраздзела можна перапісаць у выглядзе
Лічачы гэтыя суадносіны справядлівымі да ўсіх цэлых n і ненулявых b, атрымліваем
ці больш агульна,
для любой ненулявой асновы b і любога цэлага паказчыка n.
Варта адзначыць наступнае:
- Любы лік у першай ступені роўны самому сабе.
- Любы ненулявы лік у нулявой ступені роўны адзінцы; нулявы паказчык можна вытлумачыць як пусты здабытак, г.зн. здабытак, які не мае множнікаў.
- Прыведзеныя вышэй роўнасці ніяк не вызначаюць выраз 00. Гэты выраз з'яўляецца нявызначанасцю і падрабязней разглядаецца ніжэй.
- Узвядзенне нуля ў адмоўную ступень прадугледжвала б дзяленне на нуль, таму нуль у адмоўнай ступені нявызначаны.
Тоеснасць
спачатку вызначаная толькі для натуральных m і n, спраўджваецца для адвольных цэлых m і n, з тым толькі абмежаваннем, што m і n павінны быць дадатнымі, калі b — нуль.
Камбінаторнае вытлумачэнне[правіць | правіць зыходнік]
Для неадмоўных цэлых n і m, ступень nm роўная магутнасці мноства m-ак з n-элементнага мноства, або ліку ўсіх m-літарных слоў, якія можна ўтварыць з дапамогай азбукі, складзенай з n букваў.
05 = │ {} │ = 0 Няма пяцёрак з пустога мноства (азбукі). 14 = │ { (1,1,1,1) } │ = 1 Існуе адзіная чацвёрка з адналітарнай азбукі. 2³ = │ { (1,1,1), (1,1,2), (1,2,1), (1,2,2), (2,1,1), (2,1,2), (2,2,1), (2,2,2) } │ = 8 Існуе восем троек з двухэлементнага мноства. 3² = │ { (1,1), (1,2), (1,3), (2,1), (2,2), (2,3), (3,1), (3,2), (3,3) } │ = 9 Існуе дзевяць двоек з трохэлементнага мноства. 41 = │ { (1), (2), (3), (4) } │ = 4 Існуе чатыры адзінкі з чатырохэлементнага мноства. 50 = │ { () } │ = 1 Існуе адзінае пустое слова (з букваў любой азбукі).
Тоеснасці і ўласцівасці[правіць | правіць зыходнік]
- Калі аснова b не роўная нулю, наступныя тоеснасці спраўджваюцца для любых цэлых паказчыкаў m і n:
- Ступеняванне не перастаўляльнае ў адрозненне ад складання і множання. Таму, увогуле кажучы:
- Напрыклад, 2 + 3 = 3 + 2 = 5 і 2·3 = 3·2 = 6, але 23 = 8, у той час як 32 = 9.
- Ступеняванне не спалучальнае, тады як для складання і множання спалучальнасць ўласціва. У агульным выпадку:
- Напрыклад, (2 + 3) + 4 = 2 + (3 + 4) = 9 і (2·3)·4 = 2·(3·4) = 24, аднак 2³ ў 4-й ступені роўнае 84 або 4,096, а 2 ў ступені 34 роўнае 281 або 2 417 851 639 229 258 349 412 352.
Без дужак, якія змяняюць парадак вылічэнняў, па дамоўленасці парадак ступенявання зверху-ўніз, а НЕ знізу-ўверх.
Заўвага: У вышэйпрыведзенай формуле пра парадак вылічэнняў можна здагадацца дзякуючы адрозненням у памерах шрыфту, якім пададзеныя паказчыкі ступені. Тым не менш, дамоўленасць распаўсюджваецца і на радковыя запісы ўзору b^p^q = b^(p^q) ≠ (b^p)^q (такое адлюстраванне ўласціва камп'ютарным сістэмам алгебры).
Рацыянальныя паказчыкі[правіць | правіць зыходнік]
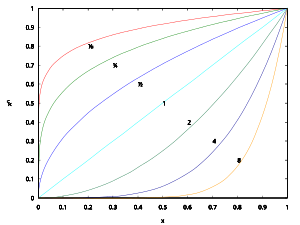
Корань n-й ступені з ліку b — такі лік x, n-ая ступень якога роўная b: xn = b.
Калі b — дадатны рэчаісны лік, а n — натуральны, тады існуе адзінае рэчаіснае рашэнне ўраўнення xn = b. Гэтае рашэнне называецца арыфметычным коранем ступені n з b. Ён абазначаецца як , дзе сімвал √ — так званы радыкал; іншым шляхам гэта можна запісаць як b1⁄n. Напрыклад: 41/2 = 2, 81/3 = 2.
Калі кажуць корань n-й ступені з дадатнага рэчаіснага ліку b, звычайна маюць на ўвазе арыфметычны корань n-й ступені.
Калі n — цотны, то ўраўненне xn = b мае два рэчаісныя рашэнні пры дадатным b: дадатны і адмоўны карані n-й ступені. Пры адмоўным b ураўненне не мае рашэнняў.
Пры няцотным n ураўненне xn = b мае адзінае рэчаіснае рашэнне. Яно дадатнае пры дадатным b і адмоўнае пры адмоўным b.
Няхай m⁄n — нескарачальны дроб.
- Пры цотных m значэнне ступені дадатнае для любых рэчаісных b.
- Калі m і n абодва няцотныя, то знак ступені супадае са знакам асновы.
- Калі ж m няцотны, а n цотны, то значэнне ступені можа быць і дадатным, і адмоўным пры дадатным b.
Прыклады: (−27)1/3 = −3, (−27)2/3 = 9, а 43/2 мае два карані 8 і −8.
Калі b адмоўны, а n цотны, пры вызначэнні ступені bm/n даводзіцца выкарыстоўваць уяўную адзінку i, як апісана ніжэй у раздзеле Ступені камплексных лікаў. Прычынай гэтага з'яўляецца адсутнасць рэчаісных рашэнняў ураўнення x² = −1.
Такім чынам, ступень рэчаіснага ліку b з рацыянальным паказчыкам m⁄n (нескарачальны дроб) можна вызначыць праз цэлую ступень і корань:
дзе m — цэлы лік, а n — натуральны лік.
Заўвага: ужываючы ступенныя тоеснасці ў выпадку адмоўнага значэння кораня n-ай ступені, нельга губляць пільнасці. Напрыклад: выснова −27 = (−27)((2/3)⋅(3/2)) = ((−27)2/3)3/2 = 93/2 = 27 відавочна няправільная. Праблема, з якой мы тут сутыкнуліся, заключаецца ў адвольнасці выбару нейкага аднаго значэння кораня з мноства магчымых яго значэнняў. Яшчэ выразней гэта ж праблема выяўляецца пры вызначэнні ступеней камплексных лікаў (гл. раздзел Няздатнасць ступенных і лагарыфмічных тоеснасцей). З гэтай прычыны ў якасці значэння кораня n-ай ступені варта браць значэнне арыфметычнага кораня.
Рэчаісныя паказчыкі[правіць | правіць зыходнік]
Прыведзеныя вышэй для цэлых паказчыкаў тоеснасці і ўласцівасці спраўджваюцца таксама і для дадатных рэчаісных лікаў з няцэлымі паказчыкамі. Аднак тоеснасць
нельга пашырыць на адмоўныя рэчаісныя асновы b (гл. Рэчаіснае ступеняванне з адмоўнымі асновамі). Непрыдатнасць гэтай тоеснасці ляжыць у аснове праблем са ступенямі камплексных лікаў, разгледжаных падрабязней у раздзеле Непрыдатнасць ступенных і лагарыфмічных тоеснасцей.
Пашырэнне ступенявання на рэчаісныя паказчыкі можна ажыццявіць або непарыўна працягваючы рацыянальныя ступені да рэчаісных, або выкарыстоўваючы паказнікавую функцыю і адваротны ёй натуральны лагарыфм.
Граніцы рацыянальных ступеней[правіць | правіць зыходнік]
А раз ірацыянальны лік можна прыблізіць рацыянальным, то ступеняванне дадатнага рэчаіснага ліку b с адвольным рэчаісным паказчыкам x можна вызначыць непарыўным працягам згодна з правілам[2]
дзе граніца бярэцца па r, якія імкнуцца да x, прабягаючы рацыянальныя значэнні. Гэта граніца існуе толькі для дадатных b. З (ε, δ)-азначэння граніцы вынікае, што можна выбраць дастаткова малы прамежак вакол x так, што ўсе рацыянальныя ступені ўнутры яго будуць набліжаць рэчаісную ступень bx з патрэбнай дакладнасцю.
Напрыклад, няхай x = π і b > 1. Тады каб атрымаць прамежкі, якія сцягваюцца да пункта і абмежаваныя рацыянальнымі ступенямі, (дзякуючы строгай манатоннасці рацыянальных ступеней) можна выкарыстаць бесканечнае дзесятковае прадстаўленне π = 3,14159...:
Гэтыя прамежкі збягаюцца да адзінага рэчаіснага ліку, абазначанага як bπ. Гэты спосаб можна ўжываць для атрымання любой ірацыянальнай ступені ліку b. Такім чынам, функцыя f(x) = bx вызначана для любога рэчаіснага ліку x.
Паказнікавая функцыя[правіць | правіць зыходнік]
Вядомая матэматычная сталая e (таксама вядомая як лік Ойлера і прыблізна роўная 2,718) з'яўляецца асновай натуральнага лагарыфма. І хоць ступеняванне ліку e можна разгледзець такім жа чынам, як і ступеняванне ўсіх іншых рэчаісных лікаў, такі падыход пакідае па-за ўвагай некаторыя прыгожыя і карысныя ўласцівасці. Сярод іншага, гэтыя ўласцівасці дазваляюць натуральным чынам абагульніць ступеняванне ліку e на іншыя віды паказчыкаў, такія як камплексныя лікі ці, нават, матрыцы.
Як вынік, запіс ex звычайна пазначае абагульненую паказнікавую функцыю exp(x), якую можна вызначыць некалькімі раўназначнымі спосабамі, напрыклад як[3]:
Сярод іншых уласцівасцей функцыя exp(x) задавальняе паказчыкавую тоеснасць:
Паказнікавая функцыя ex вызначана пры ўсіх цэлых, дробных, рэчаісных і камплексных значэннях x. Гэтае азначэнне можна выкарыстоўваць нават пры пашырэнні ступенявання на некаторыя нялікавыя велічыні, такія як квадратныя матрыцы (у гэтым выпадку паказчыкавая тоеснасць спраўджваецца, толькі калі x і y перастаўляльныя).
А раз exp(1) = e, і функцыя exp(x) задавальняе паказчыкавую тоеснасць, то адразу атрымоўваем, што азначэнне функцыі exp(x) з дапамогай граніцы раўназначнае кратна-дамнажальнаму азначэнню ex для цэлых x, адсюль вынікае супадзенне пры ўсіх рацыянальных паказчыках, а далей праз непарыўнасць і пры ўсіх рэчаісных паказчыках.
Ступеняванне праз лагарыфмаванне[правіць | правіць зыходнік]
Натуральны лагарыфм ln(x) з'яўляецца адваротнай функцыяй да паказнікавай функцыі ex. Ён вызначаны пры b > 0 і задавальняе тоеснасць
З лагарыфмічных і паказчыкавых тоеснасцей вынікае, што для любога рэчаіснага ліку x справядліва тоеснасць
Гэту тоеснасць можна выкарыстаць[3] у якасці яшчэ аднаго азначэння рэчаіснай ступені bx, якое ўзгоднена з вышэй прыведзеным азначэннем, заснаваным на выкарыстанні рацыянальных паказчыкаў і непарыўнасці. Азначэнне ступенявання праз лагарыфмаванне шырока ўжываецца ў камплексным аналізе, гл. ніжэй.
Рэчаісныя ступені з адмоўнымі асновамі[правіць | правіць зыходнік]
Ступені дадатных рэчаісных лікаў заўсёды з'яўляецца дадатнымі рэчаіснымі лікамі. Аднак ураўненне x² = 4 мае два рашэнні: 2 і −2. Галоўным, або арыфметычным, значэннем кораня 41/2 ёсць 2, але −2 таксама дапушчальнае значэнне квадратнага кораня. Такім чынам, тут узнікае неадназначнасць. І калі ў азначэнні ступенявання дазволіць выніку гэтай аперацыі прымаць адмоўныя значэнні, то паводзіны вызначанай так ступені становяцца цяжка апісальнымі і губляюць пры гэтым шматлікія карысныя ўласцівасці.
Пры адмоўным b ні праз лагарыфмаванне, ні з дапамогай граніцы па рацыянальных паказчыках нельга вызначыць br як рэчаісны лік для ўсіх рэчаісных лікаў r. Больш таго, er з'яўляецца дадатным пры любым рэчаісным значэнні r, таму ln(b) не вызначаны для b ≤ 0.
Спосаб рацыянальных паказчыкаў нельга выкарыстаць для адмоўных значэнняў b, таму што ён заснаваны на непарыўнасці. Функцыя f(r) = br мае адзіны непарыўны працяг[2][3] з мноства рацыянальных лікаў на рэчаісныя лікі пры любым b > 0. Але пры b < 0 функцыя f(r) нават не з'яўляецца непарыўнай на мностве рацыянальных лікаў r, для якіх яна вызначана.
Напрыклад, разгледзім b = −1. Корань n-ай ступені з −1 роўны −1 пры любых няцотных натуральных n. Так што пры няцотным натуральным n маем (−1)(m/n) = −1 для няцотных m, і (−1)(m/n) = 1 маем для цотных m. Адсюль атрымліваем, што мноства рацыянальных лікаў q, для якіх (−1)q = 1, шчыльнае ў мностве рацыянальных лікаў, гэтак жа як і мноства тых q, для якіх (−1)q = −1. Гэта азначае, што функцыя (−1)q разрыўная ў любым рацыянальным ліку q, дзе яна вызначана.
Гэтыя, на першы погляд бязладныя, з'явы атрымліваюць стройнае апісанне пры пераходзе да камплексных ступеней. Так адвольныя камплексныя ступені адмоўных лікаў b можна вызначыць выбіраючы нейкае значэнне камплекснага лагарыфма ліку b.
Камплексныя ступені з дадатнымі рэчаіснымі асновамі[правіць | правіць зыходнік]
Уяўныя ступені з асновай e[правіць | правіць зыходнік]

Каб усвядоміць, што ўяўляе сабой выраз eix для рэчаісных x, варта звярнуцца да геаметрычнага сэнсу аперацый над камплекснымі лікамі і азначэння паказнікавай функцыі як граніцы. Разгледзім прамавугольны трохвугольнік (0, 1, 1 + ix/n). Пры вялікіх значэннях n гэты трохвугольнік амаль тое ж, што і кругавы сектар с малым цэнтральным вуглом, роўным x/n радыянаў. Трохвугольнікі (0, (1 + ix/n)k, (1 + ix/n)k+1) узаемна падобныя пры любых цэлых k. Так што пры досыць вялікіх n значэнні (1 + ix/n)n набліжаюцца да свайго гранічнага пункта, які ляжыць на адзінкавай акружнасці і мае палярныя каардынаты (r, θ) = (1, x) (каардыната r азначае адлегласць паміж пунктам і пачаткам каардынат, каардыната θ ёсць палярны вугал, які адлічваецца ад дадатнага прамяня рэчаіснай восі); дэкартавы каардынаты гэтага пункта роўныя (cos x, sin x). Такім чынам, маем формулу
якая называецца формулай Ойлера і звязвае ступеняванне з трыганаметрычнымі функцыямі праз камплексныя лікі.
Заўвага: прыведзеныя разважанні — не доказ формулы Ойлера, а ўсяго толькі так званыя «праўдападобныя», або «эўрыстычныя», разважанні.
Рашэнні ўраўнення ez = 1 з'яўляецца кратнымі цэлымі ад 2πi:
Ці больш агульна, калі спраўджваецца роўнасць ev = w, то любое рашэнне ўраўнення ez = w можна атрымаць складаючы v і нейкае цэлае кратнае ад 2πi:
Такім чынам, камплексная паказнікавая функцыя з'яўляецца перыядычнай функцыяй з перыядам 2πi.
Прасцей: eiπ = −1; ex + iy = ex(cos y + i sin y).
Трыганаметрычныя функцыі[правіць | правіць зыходнік]
З прыведзенай вышэй формулы Ойлера вынікае, што трыганаметрычныя функцыі сінус і косінус можна вызначыць праз паказнікавую функцыю:
Гістарычна сінус і косінус былі вызначаны з дапамогай геаметрычных паняццяў да вынаходніцтва камплексных лікаў. Дзякуючы формуле Ойлера і ўласцівасцям паказнікавай функцыі складаныя формулы трыганаметрычных функцый ад сумы можна ўключыць у адну простую паказчыкавую формулу
Выкарыстанне ступенявання з камплекснымі паказчыкамі дазваляе зводзіць трыганаметрычныя задачы да алгебраічных.
Камплексныя ступені з дадатнымі рэчаіснымі асновамі[правіць | правіць зыходнік]
Няхай b з'яўляецца дадатным рэчаісным лікам, а z ёсць камплексны лік. Тады ступень bz вызначаецца як ez·ln(b), дзе x = ln(b) з'яўляецца адзіным рашэннем ураўнення ex = b. (Такім чынам, спосаб, прыдатны для рэчаісных паказчыкаў, працуе і ў выпадку камплексных паказчыкаў).
Напрыклад:
- 2i = e i·ln(2) = cos(ln(2)) + i·sin(ln(2)) ≈ 0.76924 + 0.63896i
- ei ≈ 0.54030 + 0.84147i
- 10i ≈ −0.66820 + 0.74398i
- (e2π)i ≈ 535.49i ≈ 1
Тоеснасць , увогуле кажучы, не выконваецца для камплексных ступеней. Просты проціпрыклад:
Аб прычынах гэтай з'явы гл. раздзел #Непрыдатнасць ступенных і лагарыфмічных тоеснасцей.
Ступені камплексных лікаў[правіць | правіць зыходнік]
Спробы пашырыць ступеняванне на агульны выпадак камплексных паказчыкаў і камплексных асноў сутыкаюцца з цяжкасцямі. Пры гэтым прыйдзецца мець справу з мнагазначнымі функцыямі, якія прымаюць у пункце не адно значэнне, а адразу нейкае мноства значэнняў. Акрамя таго, адны са ступенных і лагарыфмічных тоеснасцей будуць спраўджвацца толькі з пэўнымі ўдакладненнямі, а другія наогул стануць непрыгоднымі.
Пры апісанні мнагазначных функцый натуральным чынам узнікае паняцце рыманавай паверхні. Камплексныя ступені і лагарыфмы можна разглядаць як адназначныя функцыі на адпаведных рыманавых паверхнях. Рыманава паверхня мнагазначнай функцыі мнагапластовая, гэта значыць аднаму пункту на звычайнай камплекснай плоскасці адпавядае мноства пунктаў рыманавай паверхні. Аднак можна зрабіць такі разрэз камплекснай плоскасці, што рыманава паверхня распадзецца на асобныя пласты (або лісты), прычым кожнаму пункту камплекснай плоскасці на такім пласце будзе адпавядаць не больш за адзін пункт. Выбіраючы пэўны пласт рыманавай паверхні, мы тым самым выбіраем пэўную адназначную галіну функцыі. Значэнне выбранай галіны мае разрыў уздоўж разрэзу. Таму звычайныя правілы для ступеней могуць прывесці нас да памылкі.
Паколькі камплексны лагарыфм з'яўляецца мнагазначнай функцыяй, то любая нерацыянальная ступень камплекснага ліку мае бесканечную колькасць магчымых значэнняў. Галоўнае значэнне выбіраецца з мноства ўсіх значэнняў так, каб яно супадала са значэннем звычайнай рэчаіснай ступені ў выпадку дадатных рэчаісных асноў і рэчаісных паказчыкаў.
Узвядзенне дадатных рэчаісных лікаў у камплексную ступень фармальна адрозніваецца ад узвядзення камплексных лікаў у камплексную ступень. Гэта выклікана ў першую чаргу тым, што для вызначэння першай аперацыі дастаткова звычайнага адназначнага рэчаіснага лагарыфма, у той час як для другой неабходны мнагазначны камплексны лагарыфм. Тым не менш, камплекснае ступеняванне ўключае ў сябе і ступеняванне з дадатнымі рэчаіснымі асновамі.
Цэлыя ступені камплексных лікаў[правіць | правіць зыходнік]
Пры цэлых паказчыках можна карыстацца азначэннем ступені, прыведзеным у раздзеле #Адвольныя цэлыя паказчыкі. Цэлая ступень камплекснага ліку з'яўляецца адназначнай функцыяй. Акрамя таго існуе цікавая формула для ступенявання камплексных лікаў у выпадку цэлых паказчыкаў.
Няхай n — цэлы лік, і
дзе r = |z| — модуль камплекснага ліку z, θ = arg z — аргумент ліку z.
Тады згодна з формулай Муаўра цэлую ступень ліку z можна вылічыць як[4]:
Заўвага 1: калі n = 0 прымаем па азначэнні z0 = 1.
Заўвага 2: калі z = 0 аргумент arg 0 не вызначаны.
Рацыянальныя ступені камплексных лікаў[правіць | правіць зыходнік]
Рацыянальныя ступені камплексных лікаў з'яўляюцца рашэннямі пэўных алгебраічных ураўненняў. А таму, з улікам асноўнай тэарэмы алгебры, яны заўсёды маюць канечную колькасць значэнняў.
Спярша вызначым корань n-ай ступені з камплекснага ліку. Коранем n-ай ступені з ліку z называецца любое рашэнне w ураўнення wn = z. Згодна з асноўнай теарэмай алгебры гэтае ўраўненне мае n рашэнняў (калі z = 0, то ўраўненне мае адзін n-кратны корань). Напрыклад, квадратны корань w = z1/2 з'яўляецца рашэннем ураўнення w2 = z і, адпаведна, мае два значэнні.
З формулы Муаўра вынікае, што ўсе значэнні кораня n-й ступені можна вылічыць па формуле[4]:
дзе — арыфметычны корань з абсалютнай велічыні камплекснага ліку z; arg z — галоўнае значэнне аргумента ліку z, якое належыць прамежку (−π, π].

Для любых z, не роўных нулю і бесканечнасці, гэта формула дае n розных значэнняў, якія ляжаць на акружыне радыуса і ўтвараюць правільны n-вугольнік.
Значэнне кораня n-ай ступені, роўнае
называецца галоўным значэннем. Няцяжка пераканацца, што для дадатных рэчаісных лікаў галоўнае значэнне кораня супадае з арыфметычным коранем n-ай ступені.
Нарэшце, вызначым ступень з адвольным рацыянальным паказчыкам як:
Адвольныя ступені камплексных лікаў[правіць | правіць зыходнік]
Ступеняванне ў выпадку адвольных камплексных асноў і паказчыкаў вызначаецца праз камплексны натуральны лагарыфм[4]:
дзе Ln a — камплексны лагарыфм ліку a.
Варта заўважыць: раз камплексны лагарыфм — мнагазначная функцыя, то ступеняванне камплекснага ліку, ўвогуле кажучы, з'яўляецца мнагазначнай аперацыяй.
Запішам аснову a ў паказчыкавай форме
дзе r = |a| — абсалютная велічыня (модуль) ліку a, θ = arg a — галоўнае значэнне аргумента ліку a.
З улікам таго, што Ln a = {ln r + θi + 2kπi : k - цэлы лік}, ступеняванне ліку a прымае выгляд
Адсюль відаць, што пры ірацыянальным паказчыку z ступень камплекснага ліку мае бесканечна многа значэнняў. Такім чынам, каб вылічыць пэўнае значэнне ступені, найперш трэба выбраць нейкую галіну камплекснага лагарыфма (выбраць пэўнае k).
Прыклады ступенявання камплексных лікаў
У прыведзеных прыкладах пераважна выкарыстоўваецца галоўнае значэнне лагарыфма. Абсяг вызначэння галоўнага значэння — гэта камплексная плоскасць з разрэзам уздоўж адмоўнага напрамку рэчаіснай восі і выкалатым нулём. Пры гэтым галоўнае значэнне аргумента θ належыць прамежку (−π, π]. Каб вылічыць ii, запішам i ў паказчыкавай і алгебраічнай формах:
Падстаўляючы ў формулу ступенявання, атрымліваем:
Гэткім жа чынам, каб вылічыць (−2)3 + 4i, запішам лік −2 ў паказчыкавай форме,
і выкарыстаем вышэйпрыведзеную формулу
Значэнне камплекснай ступені залежыць ад таго, якая галіна выкарыстоўваецца. Напрыклад, калі пры вылічэнні ii у якасці значэння Ln i ўзяць 5πi⁄2, значэнне ступені будзе роўным e−5π⁄2; у той час як галоўнае значэнне ступені ii, вылічанае вышэй, раўняецца e−π⁄2. Мноства ўсіх магчымых значэнняў велічыні ii задаецца як:
Такім чынам, існуе бесканечна многа магчымых значэнняў ii, па адным для кожнага цэлага k. Усе яны з'яўляецца рэчаіснымі лікамі, так што можна сказаць, што ii мае бесканечна многа рэчаісных значэнняў.
Непрыдатнасць ступенных і лагарыфмічных тоеснасцей[правіць | правіць зыходнік]
Некаторыя тоеснасці для ступеней і лагарыфмаў, справядлівыя ў выпадку рэчаісных лікаў, непрыдатныя для камплексных лікаў. Прычынай гэтага ёсць тое, што нельга вызначыць камплексныя лагарыфмы і камплексныя ступені так, каб яны былі адназначнымі і ўзгодненымі са сваімі рэчаіснымі адпаведнікамі, і захоўвалі пры гэтым усе свае суадносіны, справядлівыя ў рэчаісным выпадку.
Прыклады непрыдатнасці тоеснасцей:
- Тоеснасць ln(bx) = x · ln b праўдзіцца пры любых дадатных рэчаісных b і любых рэчаісных x. Аднак для галоўнай галіны камплекснага лагарыфма ма́ем
- Тоеснасць не будзе выконвацца, якую б галіну лагарыфма мы не ўзялі. З вышэйпрыведзенага прыклада можна было б зрабіць выснову, што:
- Але гэта тоеснасць таксама несправядлівая, калі разглядаць ln(x) як мнагазначную функцыю. Магчымыя значэнні велічыні ln(wz) утрымліваюць значэнні z · ln w як падмноства. Няхай цяпер ln(x) абазначае галоўнае значэнне лагарыфма, а Ln(x) — мноства ўсіх магчымых значэнняў лагарыфма. Тады
- Тоеснасці (bc)x = bxcx і (b/c)x = bx/cx спраўджваюцца, калі b і c з'яўляецца дадатнымі рэчаіснымі лікамі, а x з'яўляецца рэчаісным лікам. Аднак, калі пры вылічэнні ступеней выкарыстоўваць галоўныя значэнні, можна атрымаць наступныя супярэчнасці:
- З другога боку, калі x — цэлы лік, тоеснасці справядлівыя для ўсіх ненулявых камплексных лікаў.
- Тоеснасць (ex)y = exy справядліва для ўсіх рэчаісных лікаў x і y. Але дапушчэнне справядлівасці тоеснасці і для камплексных лікаў прыводзіць да супярэчнасці, заўважанай у 1827 годзе Томасам Клаўзенам[5]:
- Для любога цэлага n маем:
- Але гэта няпраўда для любога n, не роўнага нулю.
- У прыведзеным разважанні паўстае шэраг праблем:
- Галоўная памылка — гэта змена парадку ступенявання пры пераходзе ад другога радка да трэцяга: якое са значэнняў выбіраецца ў якасці галоўнага.
- Аднак з погляду мнагазначнасці першая памылка была зроблена раней. У першым радку лік e разглядаецца як рэчаісны, тады як вынік e1+2πin з'яўляецца камплексным лікам, які лепш запісаць у выглядзе e+0i. Падстаноўка камплекснага ліку замест рэчаіснага ў другім радку надае ступені мнагазначнасць. Змена парадку ступенявання пры пераходзе ад другога радка да трэцяга таксама ўплывае на мноства значэнняў выніку. Таму , а дакладней спраўджваецца роўнасць , дзе апошні выраз прымае розныя значэнні ў залежнасці ад цэлых n.
- Для любога цэлага n маем:
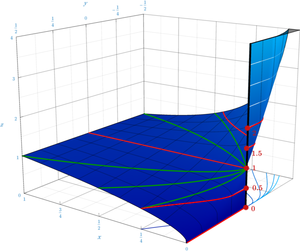
Нуль у нулявой ступені[правіць | правіць зыходнік]
Дыскрэтныя паказчыкі ступені[правіць | правіць зыходнік]
Часцей за ўсё, у абставінах, дзе паказчыкі прымаюць дыскрэтныя (звычайна, цэлыя) значэнні, вытлумачэнне значэння 00 як адзінкі спрашчае формулы і здымае патрэбу ва ўвядзенні адмысловых выпадкаў у тэарэмах. (Гл. наступны падраздзел пра абставіны, дзе паказчыкі прымаюць значэнні з непарыўнага мноства.) Напрыклад:
- Разгляд выразу b0 як пустога здабытку надзяляе яго значэннем 1, нават калі b = 0.
- У камбінаторыцы выраз 00 тлумачыцца як колькасць пустых 0-ак (нулёвак), складзеных з элементаў пустога мноства. Існуе адзіная пустая нулёўка.
- Гэтак жа тэорыя мностваў вытлумачвае выраз 00 як лік функцый з пустога мноства ў пустое. Існуе адзіная такая функцыя[6], а іменна пустая функцыя[7].
- Пішучы для мнагачленаў і ступенных радоў, мяркуюць, што 00 = 1. Тоеснасці на ўзор і , а таксама біном Ньютана справядлівыя для x = 0 толькі пры ўмове 00 = 1 [8].
- У дыферэнцыяльным злічэнні правіла дыферэнцавання ступеневай функцыі выконваецца для n = 1 у пункце x = 0 толькі пры ўмове 00 = 1.
У аналізе[правіць | правіць зыходнік]
З другога боку, калі выраз 00 узнікае пры спробе вызначыць граніцу , яго трэба разглядаць як нявызначанасць.
- Граніцу выразу часта можна вылічыць, замяніўшы падвыразы іхнімі граніцамі, ці проста падставіўшы гранічныя значэнні аргумента. Калі ж выраз пры такой падстаноўцы страчвае сэнс, яго называюць нявызначанасцю[1]. На самай справе, калі f(t) і g(t) з'яўляецца рэчаіснымі функцыямі і абедзве імкнуцца да 0 (пры t, накіраваным да рэчаіснага ліку або ±∞), і акрамя таго f(t)>0, функцыя f(t)g(t) не абавязана імкнуцца да 1. У залежнасці ад f і g, граніца выразу f(t)g(t) можа быць любым неадмоўным рэчаісным лікам або +∞, ці можа проста не існаваць. Напрыклад, усе прыведзеныя ніжэй функцыі выглядаюць як f(t)g(t), дзе f(t),g(t) → 0 пры t → 0+, аднак іхнія гранічныя значэнні розныя:
- .
- Такім чынам, выраз 00 з'яўляецца нявызначанасцю. Такія паводзіны паказваюць, што функцыя ад двух зменных xy, хоць і непарыўная на мностве {(x,y): x > 0}, але не можа быць непарыўна працягнута ні на адно мноства, якое ўтрымлівае пункт (0,0), бо няма спосабу несупярэчліва вызначыць 00.
- На камплекснай плоскасці функцыя f(z,w) = zw вызначаецца для ненулявых z згодна з zw = ew Ln z. Аднак ніводная галіна функцыі Ln z не вызначана ў пункце z = 0.
Зноскі[правіць | правіць зыходнік]
- ↑ а б в Матэматычная энцыклапедыя / Гал. рэд. В. Бернік. — Мінск: Тэхналогія, 2001.
- ↑ а б Г.М. Фихтенгольц. Курс дифференциального и интегрального исчисления. — Москва: Наука, 1966. — Т. 1. — С. 37-39.
- ↑ а б в Энциклопедия элементарной математики / Под ред. П.С. Александрова, А.И. Маркушевича и А.Я. Хинчина. — Москва - Ленинград: ГТТИ, 1952. — Т. 3 (Функции и пределы).
- ↑ а б в Маркушевич А.И. Теория аналитических функций.. — Т. 1 (Начала теории).
- ↑ Steiner J, Clausen T, Abel NH. Aufgaben und Lehrsätze, erstere aufzulösen, letztere zu beweisen // Journal für die reine und angewandte Mathematik. — 1827. — Т. 2. — С. 286–287.
- ↑ Н. Бурбаки. Начала математики. Теория множеств.. — Москва: Мир, 1965. III.§ 3.5
- ↑ якая пералівае з пустога ў парожняе :)
- ↑ «Некаторыя падручнікі пакідаюць велічыню 00 нявызначанай з тае прычыны, што функцыі x0 і 0x маюць розныя гранічныя значэнні, калі x імкнецца да 0. Але гэта памылка. Неабходна вызначыць x0 = 1 пры ўсіх x дзеля таго, каб біномная тэарэма спраўджвалася, калі x = 0, y = 0, і/або x = −y. Біномная тэарэма завельмі важная, каб яе адвольна абмяжоўваць! І, наадварот, функцыя 0x зусім неістотная». Рональд Грэхэм, Дональд Кнут, Орэн Паташник. "Биномиальные коэффициенты" // Конкретная математика. Основание информатики. — Москва: Мир, 1998. — С. 188. — ISBN 5-03-001793-3.
Літаратура[правіць | правіць зыходнік]
- Гусак А. А. Ступе́нь // Беларуская энцыклапедыя: У 18 т. Т. 15: Следавікі — Трыо / Рэдкал.: Г. П. Пашкоў і інш. — Мн. : БелЭн, 2002. — Т. 15. — С. 224. — 10 000 экз. — ISBN 985-11-0035-8. — ISBN 985-11-0251-2 (т. 15).











![{\displaystyle \scriptstyle {\sqrt[{\text{паказчык}}]{\scriptstyle {\text{падкаранёвы выраз}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c32f318a7a54a6b0726409a345eb29cee68b1bf)















![{\displaystyle {\sqrt[{n}]{b}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9a67075d2bf5949cd4927199b5ad24ee5d609b0)

![{\displaystyle b^{\frac {m}{n}}=\left(b^{m}\right)^{\frac {1}{n}}={\sqrt[{n}]{b^{m}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13a4d47568de6b9f5436c829df69e5305b4ecb49)


![{\displaystyle [b^{3},b^{4}],\ [b^{3.1},b^{3.2}],\ [b^{3.14},b^{3.15}],\ [b^{3.141},b^{3.142}],\ [b^{3.1415},b^{3.1416}],\ [b^{3.14159},b^{3.14160}],\ \ldots .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b892660185e57798c9b74e3261ad3b1e30f20f8d)













![{\displaystyle w={\sqrt[{n}]{z}}={\underset {+}{\sqrt[{n}]{|z|}}}\left(\cos \left({\frac {\arg z+2k\pi }{n}}\right)+i\sin \left({\frac {\arg z+2k\pi }{n}}\right)\right),\qquad k=0,1,\dots ,n-1,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de45d76432ff49c344cd378d624277bd81229c47)
![{\displaystyle \scriptstyle {\underset {+}{\sqrt[{n}]{|z|}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b1b0ebbf3f865ff0c83f56cce091be95f25f25)
![{\displaystyle {\underset {+}{\sqrt[{n}]{z}}}={\underset {+}{\sqrt[{n}]{|z|}}}\left(\cos {\frac {\arg z}{n}}+i\sin {\frac {\arg z}{n}}\right),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a83e073dc5e436aa25bbc8d11448980b334e9fbd)
![{\displaystyle z^{\frac {m}{n}}=\left({\sqrt[{n}]{z}}\right)^{m}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/377a460bfa563763e5c942acdb597994f1d959ac)








![{\displaystyle i\pi =\ln(-1)=\ln \left[(-i)^{2}\right]\neq 2\ln(-i)=2\left(-{\frac {i\pi }{2}}\right)=-i\pi }](https://wikimedia.org/api/rest_v1/media/math/render/svg/62be2fd4350519ed55bde61bed5a33c3f9d1ae3d)

















