Закон Архімеда
Закон Архімеда — адзін з галоўных законаў гідрастатыкі і статыкі газаў.
Фармулёўка і тлумачэнні[правіць | правіць зыходнік]
Закон Архімеда фармулюецца наступным чынам[1]: на цела, пагружанае ў вадкасць, дзейнічае сіла, якая выштурхвае яго, роўная вазе выцесненай гэтым целам вадкасці (або газу). Сіла называецца сілай Архімеда:
дзе — шчыльнасць вадкасці (газу), — паскарэнне свабоднага падзення, а — аб'ём пагружанага цела (або частка аб'ёму цела, якая знаходзіцца ніжэй паверхні). Калі цела плавае на паверхні або раўнамерна рухаецца уверх ці ўніз, то сіла (званая таксама архімедавай сілай) роўная па модулю (і процілеглая па напрамку) сіле цяжару, якая дзейнічала на выцеснены целам аб'ём вадкасці (газу), і прыкладзеная да цэнтра мас гэтага аб'ёму.
Варта заўважыць, што цела павінна быць цалкам акружана вадкасцю (альбо перасякацца з паверхняй вадкасці). Так, напрыклад, закон Архімеда нельга прымяніць да кубіка, які ляжыць на дне рэзервуара, герметычна дакранаючыся дна.
Што тычыцца цела, якое знаходзіцца ў газе, напрыклад у паветры, то для знаходжання пад'ёмнай сілы трэба замяніць шчыльнасць вадкасці на шчыльнасць газу. Напрыклад, шарык з геліем ляціць уверх з-за таго, што шчыльнасць гелію менш, чым шчыльнасць паветра.
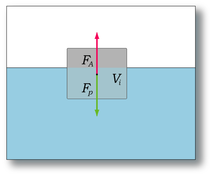
Закон Архімеда можна растлумачыць пры дапамозе рознасці гідрастатычнага ціску на прыкладзе прастакутнага цела.
дзе PA, PB — ціскі ў пунктах A і B, ρ — шчыльнасць вадкасці, h — розніца узроўняў паміж пунктамі A і B, S — плошча гарызантальнага папярочнага сячэння цела, V — аб'ём пагружанай часткі цела.
У тэарэтычнай фізіцы таксама ўжываюць закон Архімеда ў інтэгральнай форме:
- ,
дзе — плошча паверхні, — ціск у адвольным пункце, інтэграванне вырабляецца па ўсёй паверхні цела.
У адсутнасць гравітацыйнага поля, гэта значыць у стане бязважкасці, закон Архімеда не працуе. Касманаўты з гэтай з'явай знаёмыя дастаткова добра. У прыватнасці, у бязважкасці адсутнічае з'ява (натуральнай) канвекцыі, таму, напрыклад, паветранае астуджэнне і вентыляцыя жылых адсекаў касмічных апаратаў вырабляюцца прымусова, вентылятарамі.
Абагульненні[правіць | правіць зыходнік]
Нейкі аналаг закона Архімеда справядлівы таксама ў любым поле сіл, якое па-рознаму дзейнічаюць на цела і на вадкасць (газ), альбо ў неаднастайным полі. Напрыклад, гэта адносіцца да поля сіл інерцыі (напрыклад, цэнтрабежнай сілы) — на гэтым заснавана цэнтрыфугаванне. Прыклад для поля немеханічнай прыроды: діамагнетык ў вакууме выцясняецца з вобласці магнітнага поля большай інтэнсіўнасці ў вобласць з меншай.
Вывад закона Архімеда для цела адвольнай формы[правіць | правіць зыходнік]
Гідрастатычны ціск вадкасці на глыбіні ёсць . Пры гэтым лічым шчыльнасць вадкасці і напружанасць гравітацыйнага поля сталымі велічынямі, а — параметрам. Возьмем цела адвольнай формы, якое мае ненулявы аб'ём. Увядзем правую ортанарміраваную сістэму каардынатаў , прычым абярэм кірунак восі супадальным з кірункам вектару . Нуль па восі ўсталюем на паверхні вадкасці. Вылучым на паверхні цела элементарную пляцоўку . На яе будзе дзейнічаць сіла ціску вадкасці? накіраваная ўнутр цела, . Каб атрымаць сілу, якая будзе дзейнічаць на цела, возьмем інтэграл па паверхні:
Пры пераходзе ад інтэграла па паверхні да інтэгралу па аб'ёму карыстаемся абагульненай тэарэмай Астраградскага-Гауса.
Атрымліваем, што модуль сілы Архімеда роўны , а накіравана яна ў бок, процілеглы кірунку вектара напружанасці гравітацыйнага поля.
Умова плавання цел[правіць | правіць зыходнік]
Паводзіны цела, якое знаходзіцца ў вадкасці або газе, залежыць ад суадносін паміж модулямі сілы цяжару і сілы Архімеда , якія дзейнічаюць на гэтае цела. Магчымыя наступныя тры выпадкі:
- — цела тоне;
- — цела плавае ў вадкасці або газе;
- — цела ўсплывае да таго часу, пакуль не пачне плаваць.
Іншая фармулёўка (дзе — шчыльнасць цела, — шчыльнасць асяроддзя, у якую яно пагружана):
- — цела тоне;
- — цела плавае ў вадкасці або газе;
- — цела ўсплывае да таго часу, пакуль не пачне плаваць.
Гл. таксама[правіць | правіць зыходнік]
Заўвагі[правіць | правіць зыходнік]
- ↑ Усё напісанае ніжэй, калі не агаворана іншае, адносіцца да аднароднага поля сілы цяжару (напрыклад, зблізку паверхні планеты).
Спасылкі[правіць | правіць зыходнік]
- Архімедаў закон // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.) (руск.). — СПб., 1890—1907.





























