Лінейны дыскрымінантны аналіз

Лінейны дыскрымінантны аналіз (англ.: Linear discriminant analysis, LDA), нармальны дыскрымінантны аналіз (англ.: Normal discriminant analysis, NDA), або аналіз дыскрымінантнай функцыі (англ.: Discriminant function analysis) — абагульненне лінейнага дыскрымінанта Фішэра, метаду, які выкарыстоўваецца ў статыстыцы і іншых навуках, каб знайсці лінейную камбінацыю прыкмет, якая характарызуе або падзяляе два ці больш класы аб’ектаў або падзей. Атрыманая камбінацыя можа выкарыстоўвацца ў якасці лінейнага класіфікатара або, часцей, для зніжэння памернасці перад наступнай класіфікацыяй.

LDA цесна звязаны з дысперсійным аналізам (ANOVA) і рэгрэсійным аналізам, якія таксама спрабуюць выразіць адну залежную зменную як лінейную камбінацыю іншых прыкмет або вымярэнняў. Аднак ANOVA выкарыстоўвае катэгарыяльныя незалежныя зменныя і непарыўную залежную зменную, у той час як дыскрымінантны аналіз мае непарыўныя незалежныя зменныя і катэгарыяльную залежную зменную (г.зн. метку класа). Лагістычная рэгрэсія і пробіт рэгрэсія больш падобныя да LDA, чым ANOVA, бо яны таксама тлумачаць катэгарыяльную зменную значэннямі непарыўных незалежных зменных. Гэтым метадам аддаецца перавага, калі нельга меркаваць, што незалежныя зменныя маюць нармальнае размеркаванне, што з’яўляецца фундаментальным дапушчэннем метаду LDA.

LDA таксама цесна звязаны з метадам галоўных кампанентаў (PCA) і фактарным аналізам у тым, што яны ўсе шукаюць лінейныя камбінацыі зменных, якія лепш за ўсё тлумачаць даныя. LDA відавочна спрабуе змадэляваць розніцу паміж класамі даных. PCA, наадварот, не ўлічвае ніякай розніцы ў класе, а фактарны аналіз стварае камбінацыі прыкмет на аснове адрозненняў, а не падабенстваў. Дыскрымінантны аналіз таксама адрозніваецца ад фактарнага аналізу тым, што ён не з’яўляецца метадам узаемазалежнасці: неабходна адрозніваць незалежныя зменныя і залежныя зменныя (таксама называныя крытэрыяльнымі зменнымі).

LDA працуе, калі вымярэнні незалежных зменных для кожнага назірання прадстаўлены непарыўнымі велічынямі. Адпаведная методыка пры працы з катэгарыяльнымі незалежнымі зменнымі — дыскрымінантны аналіз адпаведнасці.

Дыскрымінантны аналіз выкарыстоўваецца, калі групы вядомыя апрыёры (у адрозненне ад кластарнага аналізу). Кожны выпадак павінен мець ацэнку аднаго або некалькіх колькасных прэдыктыўных вымярэнняў і ацэнку групавога вымярэння. Кажучы простымі словамі, аналіз дыскрымінантнай функцыі гэта класіфікацыя — акт размеркавання рэчаў на групы, класы або катэгорыі аднаго тыпу.

Гісторыя

Арыгінальны дыхатамічны дыскрымінантны аналіз быў распрацаваны Рональдам Фішэрам у 1936 годзе. Ён адрозніваецца ад ANOVA і MANOVA, якія выкарыстоўваюцца для прагназавання адной (ANOVA) або некалькіх (MANOVA) непарыўных залежных зменных паводле адной або некалькіх незалежных катэгарыяльных зменных. Аналіз дыскрымінантнай функцыі карысны для вызначэння таго, ці эфектыўны набор зменных для прагназавання прыналежнасці да катэгорыі.

Дапушчэнні

Дапушчэнні дыскрымінантнага аналізу такія ж, як і для MANOVA. Аналіз вельмі адчувальны да выкідаў, і памер найменшай групы павінен быць большы за колькасць прэдыктарных зменных.

• Многавымерная нармальнасць: незалежныя зменныя размеркаваны нармальна для кожнай групы.
• Гамагеннасць дысперсіі/каварыяцыі (гомаскедастычнасць): дысперсіі зменных аднолькавыя для ўсіх груп. Можна праверыць з дапамогай M-крытэрыя Бокса. Было прапанавана, аднак, выкарыстоўваць лінейны дыскрымінантны аналіз калі каварыяцыі роўныя, і квадратычны дыскрымінантны аналіз у іншым выпадку.
• Мультыкалінеарнасць: прагназавальная здольнасць можа змяншацца з павелічэннем карэляцыі паміж прэдыктарнымі зменнымі.
• Незалежнасць: мяркуецца, што аб’екты адбіраюцца выпадкова, а значэнне адной зменнай аб’екта ўважаецца незалежным ад значэнняў гэтай зменнай для ўсіх астатніх аб’ектаў.

Была выказана здагадка, што дыскрымінантны аналіз адносна трывалы да нязначных парушэнняў гэтых дапушчэнняў, а таксама было паказана, што дыскрымінантны аналіз усё яшчэ можа быць надзейным пры выкарыстанні бінарных зменных (дзе часта парушаецца многавымерная нармальнасць).

LDA для двух класаў

Разгледзім набор назіранняў ${\vec {x}}$ (таксама званых прыкметамі, атрыбутамі, зменнымі або вымярэннямі) для кожнага аб’екта або падзеі з вядомым класам $y\in \{0,1\}$. Гэты набор аб’ектаў завецца трэніровачным наборам. Праблема класіфікацыі заключаецца ў тым, каб знайсці добры крытэрый аднясення да класа $y$ любога аб’екта з аналагічным размеркаваннем (неабавязкова з трэніровачнага набору) як функцыю толькі ад назірання ${\vec {x}}$^:338.

LDA падыходзіць да праблемы з дапушчэннем, што функцыі шчыльнасці ўмоўнай імавернасці $p({\vec {x}}|y=0)$ і $p({\vec {x}}|y=1)$ адпавядаюць многавымернаму нармальнаму размеркаванню з сярэднім і матрыцай каварыяцыі $\left({\vec {\mu }}_{0},\Sigma _{0}\right)$ і $\left({\vec {\mu }}_{1},\Sigma _{1}\right)$ адпаведна. Згодна з гэтым дапушчэннем, аптымальнае рашэнне заключаецца ў аднясенні пунктаў да класа $1$, калі лагарыфм суадносін праўдападобнасцяў большы за некаторае парогавае значэнне $T$:

$({\vec {x}}-{\vec {\mu }}_{0})^{\mathrm {T} }\Sigma _{0}^{-1}({\vec {x}}-{\vec {\mu }}_{0})+\ln |\Sigma _{0}|-({\vec {x}}-{\vec {\mu }}_{1})^{\mathrm {T} }\Sigma _{1}^{-1}({\vec {x}}-{\vec {\mu }}_{1})-\ln |\Sigma _{1}|\ >\ T$

Без дадатковых дапушчэнняў атрыманы класіфікатар называецца квадратычным дыскрымінантным аналізам (QDA).

Аднак LDA робіць дадатковае спрашчальнае дапушчэнне гомаскедастычнасці (г.зн. што каварыяцыі класаў аднолькавыя, таму $\Sigma _{0}=\Sigma _{1}=\Sigma$) і што матрыцы каварыяцыі незвыродныя. У гэтым выпадку некалькі складнікаў скарачаюцца:

${\vec {x}}^{\mathrm {T} }\Sigma _{0}^{-1}{\vec {x}}={\vec {x}}^{\mathrm {T} }\Sigma _{1}^{-1}{\vec {x}}$

${\vec {x}}^{\mathrm {T} }{\Sigma _{i}}^{-1}{\vec {\mu }}_{i}={{\vec {\mu }}_{i}}^{\mathrm {T} }{\Sigma _{i}}^{-1}{\vec {x}}$, бо $\Sigma _{i}$ — сіметрычная матрыца

і прыведзены вышэй крытэрый прымае наступную форму:

${\vec {w}}^{\mathrm {T} }{\vec {x}}>c$

для некаторай парогавай канстанты $c$, дзе (для $T=0$, што эквівалентна метаду максімальнай праўдападобнасці):

${\vec {w}}=\Sigma ^{-1}({\vec {\mu }}_{1}-{\vec {\mu }}_{0})$

$c={\frac {1}{2}}\,{\vec {w}}^{\mathrm {T} }({\vec {\mu }}_{1}+{\vec {\mu }}_{0})$

Гэта значыць, што крытэрый таго, што аб’ект ${\vec {x}}$ належыць класу $y$ гэта функцыя лінейнай камбінацыі вядомых назіранняў.

Часта бывае карысна паглядзець на гэта з геаметрычнага пункта гледжання: крытэрый таго, што ${\vec {x}}$ належыць класу $y$ гэта функцыя праекцыі пункта мнагамернай прасторы ${\vec {x}}$ на вектар ${\vec {w}}$ (такім чынам, мы ўлічваем толькі кірунак ${\vec {w}}$). Іншымі словамі, назіранне належыць да $y$, калі адпаведны ${\vec {x}}$ знаходзіцца на пэўным баку гіперплоскасці, артаганальнай ${\vec {w}}$. Размяшчэнне плоскасці вызначаецца парогавым значэннем $c$.

Правілы дыскрымінацыі

• Максімальная праўдападобнасць: прысвойвае $x$ групе, для якой шчыльнасць $f_{i}(x)$ размеркавання незалежных зменных у пункце $x$ найбольшая.
• Баесаўскае правіла дыскрымінацыі: прысвойвае $x$ групе, якая максімізуе $\pi _{i}f_{i}(x)$, дзе $\pi _{i}$ уяўляе сабой апрыёрную імавернасць $i$-й групы, а $f_{i}(x)$ адлюстроўвае шчыльнасць размеркавання незалежных зменных.
• Правіла лінейнага дыскрымінанта Фішэра: максімізуе суадносіны паміж $\sigma _{\text{between}}^{2}$ і $\sigma _{\text{within}}^{2}$ і знаходзіць лінейную камбінацыю прэдыктараў для прагназавання групы.

Лінейны дыскрымінант Фішэра

Тэрміны «лінейны дыскрымінант Фішэра» і «LDA» часта выкарыстоўваюцца як узаемазамяняльныя, хаця ў арыгінальным артыкуле Фішэра апісваецца крыху іншы метад, які не робіць некаторыя дапушчэнні LDA, такія як нармальна размеркаваныя класы або роўныя класавыя каварыяцыі.

Няхай два класы назіранняў маюць сярэднія ${\vec {\mu }}_{0},{\vec {\mu }}_{1}$ і каварыяцыі $\Sigma _{0},\Sigma _{1}$. Тады лінейная камбінацыя прыкмет ${\vec {w}}^{\mathrm {T} }{\vec {x}}$ будзе мець сярэдняе ${\vec {w}}^{\mathrm {T} }{\vec {\mu }}_{i}$ і дысперсію ${\vec {w}}^{\mathrm {T} }\Sigma _{i}{\vec {w}}$ для $i=0,1$. Фішэр вызначыў падзел паміж гэтымі двума размеркаваннямі як суадносіны дысперсіі паміж класамі да дысперсіі ўнутры класаў:

$S={\frac {\sigma _{\text{between}}^{2}}{\sigma _{\text{within}}^{2}}}={\frac {({\vec {w}}\cdot {\vec {\mu }}_{1}-{\vec {w}}\cdot {\vec {\mu }}_{0})^{2}}{{\vec {w}}^{\mathrm {T} }\Sigma _{1}{\vec {w}}+{\vec {w}}^{\mathrm {T} }\Sigma _{0}{\vec {w}}}}={\frac {({\vec {w}}\cdot ({\vec {\mu }}_{1}-{\vec {\mu }}_{0}))^{2}}{{\vec {w}}^{\mathrm {T} }(\Sigma _{0}+\Sigma _{1}){\vec {w}}}}$

Гэтая мера ў пэўным сэнсе з’яўляецца мерай прапорцыі сігнал/шум для падзелу на групы. Можна паказаць, што максімальны падзел дасягаецца пры

${\vec {w}}\propto (\Sigma _{0}+\Sigma _{1})^{-1}({\vec {\mu }}_{1}-{\vec {\mu }}_{0})$.

Калі дапушчэнні LDA выкананы, прыведзенае вышэй ураўненне эквівалентна LDA.

Лінейны дыскрымінант Фішэра, адлюстраваны ў выглядзе восі

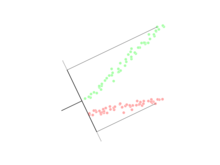
Звярніце ўвагу, што вектар ${\vec {w}}$ — нармаль да дыскрымінантнай гіперплоскасці. Напрыклад, у двухмернай задачы лінія, якая лепш за ўсё падзяляе дзве групы, перпендыкулярная да ${\vec {w}}$.

Як правіла, пункты даных, якія трэба адрозніць, праецыруюцца на ${\vec {w}}$; тады парогавае значэнне, якое лепш за ўсё падзяляе даныя, выбіраецца з аналізу аднамернага размеркавання. Агульнага правіла для парога не існуе. Аднак, калі праекцыі пунктаў з абодвух класаў маюць падобныя размеркаванні, добрым выбарам будзе гіперплоскасць паміж праекцыямі двух сярэдніх, ${\vec {w}}\cdot {\vec {\mu }}_{0}$ і ${\vec {w}}\cdot {\vec {\mu }}_{1}$. У гэтым выпадку парогавае значэнне $c$ для няроўнасці ${\vec {w}}\cdot {\vec {x}}>c$ можа быць знойдзена яўна:

$c={\vec {w}}\cdot {\frac {1}{2}}({\vec {\mu }}_{0}+{\vec {\mu }}_{1})={\frac {1}{2}}{\vec {\mu }}_{1}^{\mathrm {T} }\Sigma _{1}^{-1}{\vec {\mu }}_{1}-{\frac {1}{2}}{\vec {\mu }}_{0}^{\mathrm {T} }\Sigma _{0}^{-1}{\vec {\mu }}_{0}$.

Метад Оцу звязаны з лінейным дыскрымінантам Фішэра і быў створаны для бінарызацыі гістаграмы пікселяў на выяве ў адценнях шэрага шляхам аптымальнага выбару парога паміж чорным і белым, які мінімізуе дысперсію ўнутры класаў і павялічвае дысперсію паміж класамі (адценнямі шэрага, аднесенымі для чорнага і белага класаў пікселяў).

Мнагакласавы LDA

Візуалізацыя восяў LDA для падыходу «адзін супраць усіх» на 4 класах у 3D

Праекцыі на лінейныя дыскрымінантныя восі для 4 класаў

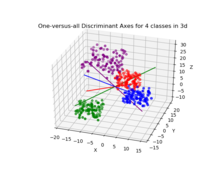
У выпадку, калі існуе больш за два класы, аналіз, які выкарыстоўваецца пры вывядзенні дыскрымінанта Фішэра, можа быць пашыраны, каб знайсці падпрастору, якая б змяшчала ўсю зменлівасць класа. Такое абагульненне прапанаваў Кальямпудзі Рао. Дапусцім, што кожны з C класаў мае сярэдняе $\mu _{i}$ і аднолькавую каварыяцыю $\Sigma$. Тады роскід паміж класамі можа быць вызначаны выбаркавай каварыяцыяй сярэдніх класаў

$\Sigma _{b}={\frac {1}{C}}\sum _{i=1}^{C}(\mu _{i}-\mu )(\mu _{i}-\mu )^{\mathrm {T} }$

дзе $\mu$ — сярэдняе значэнне класа. Падзел класаў у кірунку ${\vec {w}}$ у гэтым выпадку будзе зададзены як

$S={\frac {{\vec {w}}^{\mathrm {T} }\Sigma _{b}{\vec {w}}}{{\vec {w}}^{\mathrm {T} }\Sigma {\vec {w}}}}$

Гэта значыць, што калі ${\vec {w}}$ — уласны вектар $\Sigma ^{-1}\Sigma _{b}$, падзел S будзе роўны адпаведнаму ўласнаму значэнню.

Калі $\Sigma ^{-1}\Sigma _{b}$ можна дыяганалізаваць, зменлівасць паміж прыкметамі будзе ўтрымлівацца ў падпрасторы, ахопленай уласнымі вектарамі, адпаведнымі найбольшым уласным значэнням C − 1 (бо $\Sigma _{b}$ мае ранг не большы за C - 1). Гэтыя ўласныя вектары як правіла выкарыстоўваюцца для скарачэння колькасці прыкмет, як у PCA. Уласныя вектары, якія адпавядаюць меншым уласным значэнням, будуць вельмі адчувальныя да дакладнага выбару навучальных даных, таму часта бывае неабходна прымяняць рэгулярызацыю.

Калі патрабуецца класіфікацыя, замест зніжэння памернасці існуе шэраг альтэрнатыўных метадаў. Напрыклад, класы могуць быць згрупаваныя і стандартны дыскрымінант Фішэра або LDA выкарыстоўвацца для класіфікацыі ўнутры кожнай групы. Тыповы прыклад гэтага — метад «адзін супраць астатніх», калі аб’екты з аднаго класа дадаюцца ў адну групу, а ўсё астатняе — у другую, а пасля прымяняецца LDA. Такім чынам можна атрымаць C класіфікатараў, вынікі якіх аб’ядноўваюцца. Іншы распаўсюджаны метад — папарная класіфікацыя, пры якой новы класіфікатар ствараецца для кожнай пары класаў (агулам даючы C(C − 1)/2 класіфікатараў), з аб’яднаннем асобных класіфікатараў для атрымання канчатковай класіфікацыі.

Інкрэментны LDA

Тыповая рэалізацыя метаду LDA патрабуе, каб усе даныя былі даступныя загадзя. Аднак бываюць сітуацыі, калі ўвесь набор даных недаступны, а даныя паступаюць у выглядзе патоку. У гэтым выпадку пажадана, каб алгарытм LDA меў магчымасць абнаўляць параметры мадэлі шляхам назірання толькі за новымі аб’ектамі без запуску алгарытму на ўсім наборы даных. Напрыклад, у многіх выпадках працы ў рэжыме рэальнага часу, такіх як мабільная робататэхніка або распазнаванне твараў, важна абнаўляць параметры LDA, як толькі будуць даступныя новыя назіранні. Алгарытм, які можа абнаўляць параметры LDA шляхам назірання за новымі аб’ектамі называецца інкрэментным LDA, і шырока вывучаецца на працягу апошніх двух дзесяцігоддзяў. Чатэрджы і Ройчаўдхуры прапанавалі інкрэментны самаарганізаваны алгарытм LDA для абнаўлення параметраў. У іншай працы Дэмір і Озмехмет прапанавалі анлайн-алгарытм лакальнага навучання для паступовага абнаўлення параметраў LDA з выкарыстаннем карэкцыі памылак і правілаў навучання Хеба. Пазней Аліяры і інш. вынайшлі хуткі інкрэментны алгарытм для абнаўлення параметраў LDA.

Выкарыстанне на практыцы

На практыцы сярэднія класаў і каварыяцыі невядомыя. Іх, аднак, можна ацаніць з навучальнага набору. Замест дакладнага значэння ў прыведзеных вышэй ураўненнях можа выкарыстоўвацца або ацэнка максімальнай праўдападобнасці, або ацэнка апастэрыёрнага максімуму. Нягледзячы на тое, што ацэнкі каварыяцыі можна лічыць аптымальнымі ў некаторым сэнсе, гэта не азначае, што выніковы дыскрымінант, атрыманы падстаноўкай гэтых значэнняў, з’яўляецца аптымальным, нават калі дапушчэнне нармальнасці размеркавання класаў слушнае.

Іншая складанасць у прымяненні LDA і дыскрымінанта Фішэра да рэальных даных узнікае, калі колькасць вымярэнняў кожнага аб’екту (г.зн. памернасць кожнага вектара даных) перавышае колькасць аб’ектаў у кожным класе. У гэтым выпадку ацэнкі каварыяцыі не маюць поўнага рангу, і таму немагчыма знайсці адваротныя ім матрыцы. Ёсць некалькі спосабаў барацьбы з гэтым. Адным з іх з’яўляецца выкарыстанне псеўдаадваротнай матрыцы замест звычайнай адваротнай у прыведзеных вышэй формулах. Тым не менш, лепшая лікавая стабільнасць можа быць дасягнута, калі спачатку спраецыраваць праблему на падпрастору, ахопленую $\Sigma _{b}$. Іншая стратэгія для працы з невялікім памерам выбаркі заключаецца ў выкарыстанні сціснутай ацэнкі каварыяцыйнай матрыцы, якую можна выразіць матэматычна як

$\Sigma =(1-\lambda )\Sigma +\lambda I\,$

дзе $I$ — адзінкавая матрыца, а $\lambda$ — «інтэнсіўнасць сціскання» або «параметр рэгулярызацыі». Гэта прыводзіць да метаду рэгулярызаванага дыскрымінантнага аналізу або сціснутага дыскрымінантнага аналізу.

Акрамя таго, у многіх практычных выпадках лінейныя дыскрымінанты не пасуюць задачы. LDA і дыскрымінант Фішэра могуць быць пашыраны для выкарыстання ў нелінейнай класіфікацыі з дапамогай ядзернага труку. Тут арыгінальныя назіранні эфектыўна адлюстроўваюцца ў нелінейную прастору большай памернасці. Лінейная класіфікацыя ў гэтай нелінейнай прасторы тады эквівалентная нелінейнай класіфікацыі ў зыходнай прасторы. Найбольш часта выкарыстальным прыкладам гэтага ёсць ядзерны дыскрымінант Фішэра.

Параўнанне з лагістычнай рэгрэсіяй

Лінейны дыскрымінантны аналіз вельмі падобны да лагістычнай рэгрэсіі, і абодва алгарытмы могуць быць выкарыстаны для адказу на адны і тыя ж пытанні даследавання. Лагістычная рэгрэсія не мае столькі дапушчэнняў і абмежаванняў, як дыскрымінантны аналіз. Аднак, калі дапушчэнні дыскрымінантнага аналізу выконваюцца, ён аказваецца лепшым метадам, чым лагістычная рэгрэсія. У адрозненне ад лагістычнай рэгрэсіі, дыскрымінантны аналіз можна выкарыстоўваць для невялікіх памераў выбаркі. Было паказана, што пры роўных памерах выбаркі і аднастайнасці дысперсіі/каварыяцыі дыскрымінантны аналіз больш дакладны. Нягледзячы на ўсе гэтыя перавагі, лагістычная рэгрэсія, тым не менш, стала больш распаўсюджанай, бо дапушчэнні дыскрымінантнага аналізу рэдка выконваюцца.