Размеркаванне Бернулі

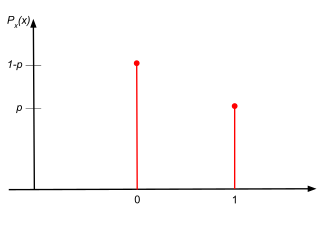
Размеркаванне Бэрнулі

Фунцыя імавернасці
Параметры	$0\leq p\leq 1,$ $q=1-p$
Носьбіт функцыі	$k\in \{0,1\}$
Функцыя імавернасці	${\begin{cases}1-p&k=0\\p&k=1\end{cases}}$
Функцыя размеркавання	${\begin{cases}0&k<0\\1-p&0\leq k<1\\1&k\geq 1\end{cases}}$
Матэматычнае спадзяванне	$p$
Медыяна	${\begin{cases}0&p<1/2\\\left[0,1\right]&p=1/2\\1&p>1/2\end{cases}}$
Мода	${\begin{cases}0&p<1/2\\0,1&p=1/2\\1&p>1/2\end{cases}}$
Дысперсія	$p(1-p)=pq$
Сярэдняе абсалютнае адхіленне	${\frac {1}{2}}$
Каэфіцыент асіметрыі	${\frac {q-p}{\sqrt {pq}}}$
Каэфіцыент эксцэсу	${\frac {1-6pq}{pq}}$
Энтрапія	$-q\ln q-p\ln p$
Утваральная функцыя момантаў	$q+pe^{t}$
Характарыстычная функцыя	$q+pe^{it}$
Імавернасная ўтваральная функцыя	$q+pz$
Інфармацыя Фішэра	${\frac {1}{pq}}$

Размеркаванне Бернулі або Бэрнулі^:81 — дыскрэтнае размеркаванне імавернасцей выпадковай велічыні, якая прымае значэнне 1 з імавернасцю $p$ і значэнне 0 з імавернасцю $q=1-p$. Прыклад размеркавання Бэрнулі — падкіданне манеты, дзе выпадзенне арла можна супаставіць значэнню 1, а рэшкі — значэнню 0. У выпадку, калі манета «сумленная», імавернасці выпадзення арла і рэшкі мусяць быць роўнымі, а значыць $p=0.5$.

Размеркаванне Бэрнулі названае ў гонар швейцарскага матэматыка Якаба Бэрнулі.

Азначэнне

Выпадковая велічыня $X$ мае размеркаванне Бэрнулі (запісваецца $X\sim Bernoulli(p)$), калі выконваецца

$P(X=1)=p,$

$P(X=0)=1-p.$

Для спрашчэння натацыі часта ўводзіцца параметр $q:=1-p.$

Функцыя імавернасці мае выгляд

$p_{X\sim Bernoulli(p)}(k)={\begin{cases}p&k=1,\\1-p&k=0.\end{cases}}$

Таксама можна запісаць

$p_{X\sim Bernoulli(p)}(k)=p^{k}(1-p)^{1-k}\quad k\in \{0,1\}$

або

$p_{X\sim Bernoulli(p)}(k)=pk+(1-p)(1-k)\quad k\in \{0,1\}.$

Характарыстыкі

Матэматычнае спадзяванне выпадковай велічыні, якая мае размеркаванне Бэрнулі, роўнае^:118

$\mathbb {E} [X]=1\cdot p+0\cdot (1-p)=p.$

Дысперсія роўная^:118

$Var(X)=\mathbb {E} [X^{2}]-\mathbb {E} [X]^{2}=1^{2}\cdot p+0^{2}\cdot (1-p)-p^{2}=p\cdot (1-p)=pq.$

Сувязь з іншымі размеркаваннямі

Біномнае размеркаванне

Размеркаванне Бэрнулі — асобны выпадак біномнага размеркавання для $n=1$^:81. Іншымі словамі, велічыня $X\sim Bernoulli(p)$ мае такое ж размеркаванне, як і велічыня $X\sim B(1,p).$