Адзінкавая акружнасць

Адзі́нкавая акру́жнасць — акружнасць з радыусам 1 і цэнтрам у пачатку каардынат.
Для каардынат (x, y) усіх пунктаў на адзінкавай акружнасці, згодна з тэарэмай Піфагора, выконваецца роўнасць:
Паняцце адзінкавай акружнасці абагульняецца да n-мернай прасторы (), у такім выпадку кажуць аб «адзінкавай сферы».
Трыганаметрычныя функцыі[правіць | правіць зыходнік]
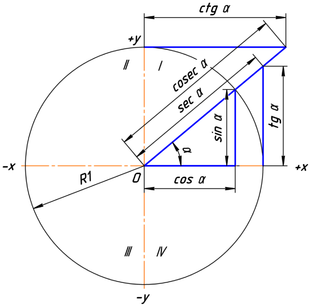
З дапамогай адзінкавай акружнасці могуць быць наглядна апісаны трыганаметрычныя функцыі.
Сінус і косінус могуць быць апісаны наступным чынам: калі злучыць любую кропку на адзінкавай акружнасці з пачаткам каардынат , атрымліваецца адрэзак, які знаходзіцца пад вуглом адносна дадатнай паўвосі абсцыс. Тады сапраўды:
Пры падстаноўцы гэтых значэнняў ва ўраўненне акружнасці атрымліваецца:
(Выкарыстоўваецца наступнае агульнапрынятае абазначэнне: .)
Тут жа наглядна апісваецца перыядычнасць трыганаметрычных функцый, бо адпаведнае вуглу становішча адрэзка не залежыць ад колькасці «поўных абаротаў»:
для ўсіх цэлых лікаў , г.зн. для .
Камплексная плоскасць[правіць | правіць зыходнік]

На камплекснай плоскасці адзінкавая акружнасць — гэта наступнае мноства :
Мноства з'яўляецца падгрупай групы камплексных лікаў па множанню, яе нейтральны элемент — гэта .


















