Тэарэма Піфагора
Артыкул вымагае праверкі арфаграфіі Удзельнік, які паставіў шаблон, не пакінуў тлумачэнняў. |

Тэарэма Піфагора — адна з асноўных тэарэм еўклідавай геаметрыі, якая вызначае сувязь паміж старанамі прамавугольнага трохвугольніка. Гэта тэарэма сцвярджае, што плошча квадрата, чый бок з’яўляецца гіпатэнузай (старана трохвугольніка, якая ляжыць насупраць прамога вугла) роўны суме плошчаў двух квадратаў, што ляжаць на астатніх старанах трохвугольніка. Гэта тэарэма можа быць запісана ўраўненнем паміж даўжынямі катэтаў a, b і гіпатэнузай c:
Гісторыя[правіць | правіць зыходнік]

У старажытнакітайскай кнізе Чжоу бі суань цзын (кіт.: 周髀算經) гаворыцца пра піфагораў трохвугольнік з бакамі 3, 4 і 5[1]. У гэтай жа кнізе прапанаваны рысунак, які супадае з адным з рысункаў індыйскай геаметрыі Басхары.
Морыц Кантар (найбуйнейшы нямецкі гісторык матэматыкі) лічыць, што роўнасць 3² + 4² = 5² была вядомая егіпцянам яшчэ каля 2300 года да н. э., у часы цара Аменемхета I (згодна з папірусам 6619 Берлінскага музея). На думку Кантара, гарпеданапты, або «нацягвачы вяровак», будавалі прамыя вуглы пры дапамозе прамавугольных трохвугольнікаў з бакамі 3, 4 і 5.
Вельмі лёгка можна паўтарыць іх спосаб будавання. Возьмем вяроўку даўжынёю ў 12 метраў і прывяжам да яе каляровыя палоскі на адлегласці 3 метры ад аднаго канца і 4 метры ад іншага. Прамы вугал апынецца паміж бакамі даўжынёй у 3 і 4 метры. Гарпеданаптам можна было б запярэчыць, што іх спосаб будавання становіцца залішнім, калі скарыстацца, напрыклад, драўляным вугольнікам, якім карыстаюцца ўсе цеслі. І сапраўды, вядомыя егіпецкія малюнкі, на якіх сустракаецца такі інструмент, — напрыклад, малюнкі, якія паказваюць сталярную майстэрню.
Крыху больш вядома пры тэарэму Піфагора ў вавіланян. У адным тэксце, які адносіцца да часоў Хамурапі, гэта значыць да 2000 года да н. э., прыводзіцца набліжанае вылічэнне гіпатэнузы роўнабаковага прамавугольнага трохвугольніка[2]. Адсюль можна зрабіць выснову, што ў Месапатаміі ўмелі рабіць вылічэнні з прамавугольнымі трохвугольнікамі, па меншай меры ў некаторых выпадках.
Грунтуючыся, з аднаго боку, на сённяшнім узроўні ведаў аб егіпецкай і вавілонскай матэматыцы, а з другога — на крытычным вывучэнні грэчаскіх крыніц, Ван-дэр-Вард (галандскі матэматык) зрабіў выснову аб вялікай імавернасці таго, што тэарэма аб квадраце гіпатэнузы была вядомая ў Вавілоне ўжо каля XVIII стагоддзя да н. э.
Згодна з каментаром Прокла да Эўкліда, Піфагор (гадамі жыцця якога прынята лічыць 570—490 гг. да н. э.) карыстаўся алгебраічнымі метадамі, каб знаходзіць піфагоравыя тройкі. Аднак Прокл пісаў паміж 410 і 485 гг. н. э. Томас Літл Хіт лічыў, што не існуе відавочных згадак, якія адносіцца да перыяду працягласцю ў пяць стагоддзяў пасля смерці Піфагора, што Піфагор быў аўтарам тэарэмы[3]. Аднак, калі аўтары, такія як Плутарх і Цыцэрон, пішуць пра тэарэму Піфагора, яны пішуць так, нібы аўтарства Піфагора было шырока вядомым і бясспрэчным[4][5]. «Ці належыць гэтая формула асабіста пяру Піфагора…, але мы можам упэўнена лічыць, што яна належыць найстаражытнейшаму перыяду піфагоравай матэматыкі»[6]. Паводле падання, Піфагор адсвяткаваў адкрыццё сваёй тэарэмы гіганцкім балем, для якога закалолі з радасці сотню быкоў[7].
Прыблізна ў 400 г. да н. э., паводле Прокла, Платон адшукаў метад знаходжання піфагоравых троек, які спалучае алгебру і геаметрыю. Прыблізна ў 300 г. да н. э. у «Пачатках» Еўкліда з’явіўся найстарэйшы аксіяматычны доказ тэарэмы Піфагора[8].
Фармулёўкі[правіць | правіць зыходнік]
Геаметрычная фармулёўка:
Першапачаткова тэарэма была сфармуляваная наступным чынам:
|
У прамавугольным трохвугольніку плошча квадрата, пабудаванага на гіпатэнузе, роўная суме плошчаў квадратаў, пабудаваных на катэтах. |
Алгебраічная фармулёўка:
|
У прамавугольным трохвугольніку квадрат даўжыні гіпатэнузы роўны суме квадратаў даўжынь катэтаў. |
Гэта значыць, пазначыўшы даўжыню гіпатэнузы трохвугольніка праз , а даўжыні катэтаў праз і :
Абедзве фармулёўкі тэарэмы эквівалентныя, але другая фармулёўка больш элементарная, яна не патрабуе паняцця плошчы. Гэта значыць другое сцверджанне можна праверыць, нічога не ведаючы пра плошчы і памераўшы толькі даўжыні бакоў прамавугольнага трохвугольніка.
Адваротная тэарэма Піфагора:
|
Для ўсякай тройкі дадатных лікаў , і , такой, што , існуе прамавугольны трохвугольнік з катэтамі і , і гіпатэнузай . |
Доказы[правіць | правіць зыходнік]
На сённяшні дзень у навуковай літаратуры зафіксавана 367 доказаў тэарэмы[9]. Імаверна, тэарэма Піфагора ёсць адзінай тэарэмай з настолькі вялікай колькасцю доказаў. Такую разнастайнасць можна патлумачыць толькі фундаментальным значэннем тэарэмы для геаметрыі.
Канцэптуальна іх можна разбіць на невялікую колькасць класаў. Самыя вядомыя з іх: доказы метадам плошчаў, аксіяматычныя і экзатычныя доказы (напрыклад, з дапамогай дыферэнцыяльных ураўненняў).
Праз падобныя трохвугольнікі[правіць | правіць зыходнік]
Гэты доказ алгебраічнай фармулёўкі — найпрасцейшы з доказаў, якія будуюцца наўпрост з аксіём. У прыватнасці, ён не выкарыстоўвае паняцце плошчы фігуры.
Няхай ABC ёсць прамавугольны трохвугольнік з прамым вуглом C. Правядзём вышыню з C і абазначым яе аснову праз H. Трохвугольнік ACH падобны да трохвугольніку ABC па двух вуглах. Аналагічна, трохвугольнік CBH падобны да ABC. Увёўшы абазначэнні
атрымаем
Што эквівалентна
Дадаўшы, атрымаем
або
- , што і патрабавалася даказаць.
Доказы метадам плошчаў[правіць | правіць зыходнік]
Ніжэй прыведзеныя доказы, нягледзячы на іх уяўную прастату, зусім не такія простыя. Усе яны выкарыстоўваюць уласцівасці плошчы, доказы якіх складаней за доказы самой тэарэмы Піфагора.
Доказ праз роўнадапаўняльнасць[правіць | правіць зыходнік]

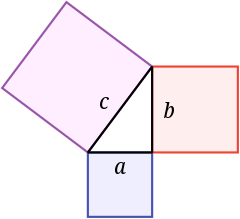
- Размесцім чатыры роўныя прамавугольныя трохвугольнікі так, як паказана на рысунку 1.
- Чатырохвугольнік з бакамі c з’яўляецца квадратам, бо сума двух вострых вуглоў роўная 90°, а разгорнуты вугал — 180°.
- Плошча ўсёй фігуры роўная, з аднаго боку, плошчы квадрата з бокам (a+b), а з другога боку, суме плошчаў чатырох трохвугольнікаў і плошчы ўнутранага квадрата.
Што і патрабавалася даказаць.
Доказ Еўкліда[правіць | правіць зыходнік]


Ідэя доказу Еўкліда складаецца ў наступным: паспрабуем даказаць, што палова плошчы квадрата, пабудаванага на гіпатэнузе, роўная суме палоў плошчаў квадратаў, пабудаваных на катэтах, а тады і плошчы вялікага і двух малых квадратаў роўныя.
Разгледзім рысунак злева. На ім мы пабудавалі квадраты на баках прамавугольнага трохвугольніка і правялі з вяршыні прамога вугла С прамень s перпендыкулярна гіпатэнузе AB, ён рассякае квадрат ABIK, пабудаваны на гіпатэнузе, на два прамавугольнікі — BHJI і HAKJ адпаведна. Аказваецца, што плошчы гэтых прамавугольнікаў роўныя плошчам квадратаў, пабудаваных на адпаведных катэтах.
Паспрабуем даказаць, што плошча квадрата DECA роўная плошчы прамавугольніка AHJK. Для гэтага скарыстаемся дапаможным назіраннем: плошча трохвугольніка з той жа вышынёй і асновай, што і гэты трохвугольнік, роўная палове плошчы зададзенага прамавугольніка. Гэта вынік вызначэння плошчы трохвугольніка як паловы здабытку асновы на вышыню. З гэтага назірання выцякае, што плошча трохвугольніка ACK роўная плошчы трохвугольніка AHK (не накрэсленага на рысунку), якая, у сваю чаргу, роўная палове плошчы прамавугольніка AHJK.
Дакажам цяпер, што плошча трохвугольніка ACK таксама роўная палове плошчы квадрата DECA. Адзінае, што неабходна для гэтага зрабіць, — гэта даказаць роўнасць трохвугольнікаў ACK і BDA (бо плошча трохвугольніка BDA роўная палове плошчы квадрата па паказанай вышэй ўласцівасці). Роўнасць гэта відавочная: трохвугольнікі роўныя па двух баках і вугле паміж імі. Менавіта — AB = AK, AD = AC — роўнасць вуглоў CAK і BAD лёгка даказаць метадам руху: павернем трохвугольнік CAK на 90° супраць гадзіннікавай стрэлкі, тады відавочна, што адпаведныя бакі двух разглядаемых трохвугольнікаў супадуць (з прычыны таго, што вугал пры вяршыні квадрата 90°).
Разважанне наконт роўнасці плошчаў квадрата BCFG і прамавугольніка BHJI аналагічнае.
Такім чынам мы даказалі, што плошча квадрата, пабудаванага на гіпатэнузе, складаецца з плошчаў квадратаў, пабудаваных на катэтах. Ідэя доказу дадаткова праілюстравана з дапамогай анімацыі, размешчанай вышэй.
Гэты доказ таксама атрымаў назву «піфагоравы штаны».
Доказ Леанарда да Вінчы[правіць | правіць зыходнік]

Галоўныя элементы доказу — сіметрыя і рух.
Разгледзім рысунак. Як відаць з сіметрыі, адрэзак CI рассякае квадрат ABHJ на дзве аднолькавыя часткі (бо трохвугольнікі ABC і JHI роўныя пабудовай).
Карыстаючыся паваротам на 90 градусаў супраць гадзіннікавай стрэлкі вакол пункту A, мы ўгледжваем роўнасць заштрыхаваных фігур CAJI і DABG.
Цяпер ясна, што плошча заштрыхаванай намі фігуры роўная суме палоў плошчаў маленькіх квадратаў (пабудаваных на катэтах) і плошчы зыходнага трохвугольніка. З іншага боку, яна роўная суме паловы плошчы вялікага квадрата (пабудаванага на гіпатэнузе) і плошчы зыходнага трохвугольніка. Такім чынам, палова сумы плошчаў маленькіх квадратаў роўная палове плошчы вялікага квадрата, а значыць сума плошчаў квадратаў, пабудаваных на катэтах роўная плошчы квадрата, пабудаванага на гіпатэнузе.
Доказ метадам бясконца малых[правіць | правіць зыходнік]
Наступны доказ пры дапамозе дыферэнцыяльных ураўненняў часта прыпісваюць вядомаму англійскаму матэматыку Хардзі, які жыў у першай палове XX стагоддзя.
Разглядаючы рысунак, і назіраючы змену боку a, мы можам запісаць роўнасць адносін для бясконца малых прыростаў бакоў с і a (выкарыстоўваючы падабенства трохвугольнікаў):
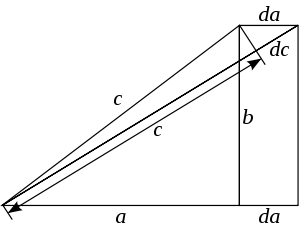
Карыстаючыся метадам падзелу зменных, знаходзім
Больш агульны выраз для змены гіпатэнузы ў выпадку прыросту абодвух катэтаў
Інтэгруючы гэтае ўраўненне і выкарыстоўваючы пачатковыя ўмовы, атрымліваем
Такім чынам, мы прыходзім да пажаданага адказу
Як няцяжка бачыць, квадратычнай залежнасць ў канчатковай формуле з’яўляецца дзякуючы лінейнай прапарцыянальнасці паміж бакамі трохвугольніка і прыростамі, у той час як сума звязана з незалежнымі ўнёскамі ад прыросту розных катэтаў.
Больш просты доказ можна атрымаць, калі лічыць, што адзін з катэтаў не змяняецца (у гэтым выпадку катэт ). Тады для канстанты інтэгравання атрымаем
Варыяцыі і абагульненні[правіць | правіць зыходнік]
Падобныя геаметрычныя фігуры на трох баках[правіць | правіць зыходнік]

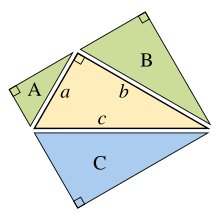
Абагульненне тэарэмы Піфагора зрабіў Еўклід у сваёй працы «Пачаткі», пашырыўшы плошчы квадратаў на баках да плошчаў падобных геаметрычных фігур[10]:
Калі пабудаваць падобныя геаметрычныя фігуры (гл. Эўклідава геаметрыя) на баках прамавугольнага трохвугольніка, тады сума двух меншых фігур будзе раўняцца плошчы большай фігуры.
Галоўная ідэя гэтага абагульнення заключаецца ў тым, што плошча падобнай геаметрычнай фігуры прапарцыянальная квадрату любога свайго лінейнага памеру і ў прыватнасці квадрату даўжыні любога боку. Такім чынам, для падобных фігур з плошчамі A, B і C пабудаваных на баках з даўжынёй a, b і c, маем:
Але, па тэарэме Піфагора, a² + b² = c², тады A + B = C.
І наадварот, калі мы зможам даказаць, што A + B = C для трох падобных геаметрычных фігур без выкарыстання тэарэмы Піфагора, тады мы зможам даказаць саму тэарэму, рухаючыся ў зваротным кірунку. Напрыклад, стартавы цэнтральны трохвугольнік можа быць паўторна выкарыстаны як трохвугольнік C на гіпатэнузы, і два падобных прамавугольных трохвугольніка (A і B), пабудаваныя на двух іншых баках, якія ўтвараюцца ў выніку дзялення цэнтральнага трохвугольніка яго вышынёй. Сума двух меншых плошчаў трохвугольнікаў тады, відавочна, роўная плошчы трэцяга, такім чынам A + B = C і, выконваючы папярэдняе даказванне ў зваротным парадку, атрымаем тэарэму Піфагора a² + b² = c².
Тэарэма косінусаў[правіць | правіць зыходнік]
Тэарэма Піфагора — гэта прыватны выпадак больш агульнай тэарэмы косінусаў, якая звязвае даўжыні бакоў у адвольным трохвугольніку:[11]
дзе θ — вугал паміж бакамі a і b.
Калі θ роўны 90 градусаў, тады cosθ = 0 і формула спрашчаецца да звычайнай тэарэмы Піфагора.
Адвольны трохвугольнік[правіць | правіць зыходнік]

У любы абраны вугал адвольнага трохвугольніка з бакамі a, b, c ўпішамся роўнабаковы трохвугольнік такім чынам, каб роўныя вуглы пры яго аснове θ былі роўныя выбраным куце. Дапусцім, што абраны вугал θ размешчаны насупраць боку, пазначанай c. У выніку мы атрымалі трохвугольнік ABD з вуглом θ, што размешчаны насупраць боку a і боку r. Другі трохвугольнік утворыцца вуглом θ, што размешчаны насупраць боку b і боку з даўжынёй s, як паказана на малюнку. Сабіт Ібн Кура[13] сцвярджаў, што бакі ў гэтых трох трохвугольніках звязаныя наступным чынам:[14][15]
Калі вугал θ набліжаецца да π/2, аснова роўнабаковага трохвугольніка памяншаецца, і два бакі r і s перакрываюць адзін аднаго ўсё менш і менш. Калі θ = π/2, ADB ператвараецца ў прамавугольны трохвугольнік, r + s = c і атрымліваем пачатковую тэарэму Піфагора.
Разгледзім адзін з довадаў. Трохвугольнік ABC мае такія ж вуглы, як і Трохвугольнік ABD, але ў зваротным парадку. (Два трохвугольніка маюць агульны вугал пры вяршыні B, абодва маюць кут θ і таксама маюць аднолькавы трэці вугал, па суме вуглоў трохвугольніка) Адпаведна, ABC — падобны да адбіцця ABD трохвугольніка DBA, як паказана на ніжнім малюнку. Запішам суадносіны паміж супрацьлеглымі бакамі і прылеглымі да вугла θ,
Гэтак жа адлюстраванне іншага трохвугольніка,
Перамнажаць дробы і дадамо гэтыя дзве суадносіны:
што і патрабавалася даказаць.
Абагульненне для адвольных трохвугольнікаў праз паралелаграмы[правіць | правіць зыходнік]
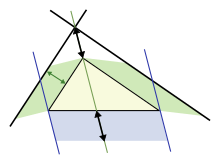
плошча зялёнага ўчастка = плошчы сіняга.

Зробім далейшае абагульненне для непрамавугольных трохвугольнікаў, выкарыстоўваючы паралелаграмы на трох баках замест квадратаў[16]. (квадраты — прыватны выпадак.) Верхні малюнак дэманструе, што для востравугольнага трохвугольніка плошчу паралелаграма на доўгім баку роўная суме паралелаграма на двух іншых баках, пры ўмове што паралелаграм на доўгай баку пабудаваны, як намалявана на малюнку (памеры, адзначаныя стрэлкамі, аднолькавыя і вызначаюць бакі ніжняга паралелаграма). Гэтая замена квадратаў паралелаграма мае дакладнае падабенства з пачатковай тэарэмай Піфагора, лічыцца, што яе сфармуляваў Пап Александрыйскі ў 4 г. н. э.[16]
Ніжні малюнак паказвае ход доказу. Паглядзім на левы бок трохвугольніка. Левы зялёны паралелаграм мае такую ж плошчу, як левая частка сіняга паралелаграма, таму што яны маюць такое ж аснова b і вышыню h. Акрамя таго, левы зялёны паралелаграм мае такую ж плошчу, як левы зялёны паралелаграм на верхнім малюнку, таму што яны маюць агульную аснова (верхняя левы бок трохвугольніка) і агульную вышыню, перпендыкулярную да гэтай баку трохвугольніка. Аналагічна разважаючы для правага боку трохвугольніка дакажам, што ніжні паралелаграм мае такую ж плошчу, як у двух зялёных паралелаграмаў.
Камплексныя лікі[правіць | правіць зыходнік]
Тэарэму Піфагора выкарыстоўваюць, каб знайсці адлегласць паміж двума пунктамі ў дэкартавай каардынатнай сістэме, і гэтая тэарэма справядлівая для ўсіх сапраўдных каардынат: адлегласць s паміж двума пунктамі (a, b) і (c, d) роўна
Не ўзнікае праблем з формулай, калі да комплексным лікаў адносіцца як да вектарах з сапраўднымі кампанентамі x + i y = (x, y). Напрыклад, адлегласць s паміж 0 + 1i і 1 + 0i разлічваем як модуль вектара (0, 1) − (1, 0) = (−1, 1), або
Тым не менш, для аперацый з вектарамі з комплекснымі каардынатамі неабходна правесці некаторае ўдасканаленне формулы Піфагора. Адлегласць паміж пунктамі з комплекснымі лікамі (a, b) і (c, d); a, b, c, і d ўсё комплексныя, сфармулюем выкарыстоўваючы абсалютныя велічыні. Адлегласць s заснавана на вектарнай розніцы (a − c, b − d) у наступным выглядзе[17]: хай розніца 'a − c = p + i q, где p — сапраўдная частка розніцы, q — уяўная частка, і i = √(−1). Аналагічна, хай b − d = r + is. Тады:
дзе — гэта комплексны спалучаны лік для . Напрыклад, адлегласць паміж пунктамі (a, b) = (0, 1) і (c, d) = (i, 0), разлічым розніцай (a − c, b − d) = (−i, 1) і ў выніку мы б атрымалі 0, калі б не былі выкарыстаныя комплексныя спалучаныя. Такім чынам, выкарыстоўваючы удасканаленую формулу, атрымаем
Модуль вызначаны наступным чынам:
што ўяўляе сабой эрмітавы скалярны здабытак[18].
Стэрэаметрыя[правіць | правіць зыходнік]
Значным абагульненнем тэарэмы Піфагора для трохмернай прасторы з’яўляецца тэарэма дэ Гуа, названая ў гонар Ж.-П. дэ Гуа: калі тэтраэдр мае прамы вугал (як у кубе), тады квадрат плошчы мяжы, якая ляжыць насупраць прамога вугла, роўны суме квадратаў плошчаў іншых трох граняў. Гэтая выснова можа быць абагульнены як «n-мерная тэарэма Піфагора»:[19]
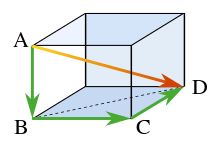
Іншае абагульненне: Тэарэма Піфагора можа быць прыменена для стэрэаметрыі ў наступным выглядзе. Разгледзім прамавугольны паралелепіпед, як паказана на малюнку. Знойдзем даўжыню дыяганалі BD па тэарэме Піфагора:
дзе тры бакі ўтвараюць прастакутны трохвугольнік. Выкарыстоўваем гарызантальную дыяганаль BD і вертыкальнае рабро AB, каб знайсці даўжыню дыяганалі AD, для гэтага зноў выкарыстоўваем тэарэму Піфагора:
або, калі ўсё запісаць адным ураўненнем:
Гэты вынік — гэта трохмерны выраз для вызначэння велічыні вектара v (дыяганаль AD), выяўленага праз яго перпендыкулярныя складнікі {vk} (тры ўзаемна перпендыкулярныя бакі):
Гэта ўраўненне можна разглядаць як абагульненне тэарэмы Піфагора для шматмернай прасторы. Аднак, вынік на самай справе ёсць не што іншае, як неаднаразовае прымяненне тэарэмы Піфагора да паслядоўнасці прамавугольных трохвугольнікаў ў паслядоўна перпендыкулярных плоскасцях.
Вектарная прастора[правіць | правіць зыходнік]
У выпадку артаганальнай сістэмы вектараў мае месца роўнасць, якое таксама называюць тэарэмай Піфагора:
Калі — гэта праекцыі вектара на каардынатныя восі, то гэтая формула супадае з адлегласцю Еўкліда — і азначае, што даўжыня вектару роўная пні квадратнага сумы квадратаў яго кампанентаў.
Аналаг гэтага роўнасці ў выпадку бясконцай сістэмы вектараў мае назву роўнасці Парсеваля.
Нееўклідава геаметрыя[правіць | правіць зыходнік]
Тэарэма Піфагора выводзіцца з аксіём еўклідавай геаметрыі і, фактычна, не сапраўдная для нееўклідавай геаметрыі, у тым выглядзе, у якім запісана вышэй[20]. (Гэта значыць тэарэма Піфагора аказваецца своеасаблівым эквівалентам пастулату Еўкліда аб паралельнасці[21][22]) Іншымі словамі, у нееўклідавай геаметрыі суадносіны паміж бакамі трохвугольніка абавязкова будзе ў форме, якая адрозніваецца ад тэарэмы Піфагора. Напрыклад, у сферычнай геаметрыі ўсе тры бакі прамавугольнага (скажам a, b і c), якія абмяжоўваюць сабой актант (восьмую частку) адзінкавай сферы, маюць даўжыню π/2, што супярэчыць тэарэме Піфагора, таму што a2 + b2 ≠ c2.
Разгледзім тут два выпадкі нееўклідавай геаметрыі — сферычная і гіпербалічныя геаметрыя; у абодвух выпадках, як і для еўклідавай прасторы для прамавугольных трохвугольнікаў, вынік, які замяняе тэарэму Піфагора, вынікае з тэарэмы косінусаў.
Аднак, тэарэма Піфагора застаецца справядлівай для гіпербалічнай і эліптычнай геаметрыі, калі патрабаванне аб прамавугольнага трохвугольніка замяніць умовай, што сума двух вуглоў трохвугольніка павінна раўняцца трэцяму, скажам A+B = C. Тады суадносіны паміж бакамі выглядае так: сума плошчаў колаў з дыяметрамі a і b роўная плошчы круга з дыяметрам c.[23]
Сферычная геаметрыя[правіць | правіць зыходнік]

Для любога прамавугольнага трохвугольніка на сферы радыусам R (напрыклад, калі вугал γ ў трыкутніку прамы) з бакамі a, b, c суадносіны паміж бакамі будуць мець такі выгляд:[24]
Гэта роўнасць можа быць выведзена як асаблівы выпадак сферычнай тэарэмы косінусаў, якая справядліва для ўсіх сферычных трохвугольнікаў:
Ужываючы рад Тэйлара ў функцыі косінуса cos x ≈ 1 − x2/2 можна паказаць, што калі радыус R набліжаецца да бясконцасці, а аргументы a/R, b/R і c/R набліжаюцца да нуля, сферычныя суадносіны паміж бакамі ў прамавугольным трохвугольніку набліжаецца да тэарэмы Піфагора. Падставім набліжаныя значэнні для кожнага косінуса:
Перамнажаць выразы ў дужках, атрымаем тэарэму Піфагора для вялікіх радыусаў R:
дзе «higher order terms» — складнікі вышэйшага парадку, якімі можна грэбаваць пры вялікіх значэннях R.
Гіпербалічныя геаметрыя[правіць | правіць зыходнік]

Для прамавугольнага трохвугольніка ў гіпербалічнай геаметрыі з бакамі a, b, c, калі бок c размешчаны насупраць прамога вугла, суадносіны паміж бакамі будуць такімі[25]
где ch — гіпербалічны косінус[26]. Гэтая формула з’яўляецца прыватным выпадкам гіпербалічнай тэарэмы косінусаў, якая справядлівая для ўсіх трохвугольнікаў:[27]
дзе — гэта вугал, вяршыня якога процілеглая баку c.
Выкарыстоўваючы рад Тэйлара для гіпербалічнага косінуса , можна даказаць, што калі гіпербалічны трохвугольнік памяншаецца (гэта значыць, калі a, b, і c набліжаюцца да нуля), то гіпербалічныя суадносіны ў прамавугольным трохвугольніку набліжаюцца да тэарэмы Піфагора.
Дыферэнцыяльная геаметрыя[правіць | правіць зыходнік]

У трохмернай прасторы для двух пунктаў, аддаленых адзін ад аднаго на бясконца малую адлегласць, запішам тэарэму Піфагора:
дзе ds — гэта адлегласць паміж пунктамі, а (dx, dy, dz) — кампаненты вектара, якія злучаюць гэтыя два пункты. Такая прастора называецца еўклідавай. Аднак, абагульненне гэтага выказвання прыдатна для агульных каардынат (не толькі дэкартавых) і агульных прастор (не толькі еўклідавай) і мае выгляд:[28]
дзе gij называецца метрычным тэнзарам. Ён можа быць функцыяй пазіцыі. Такія крывалінейныя прасторы ўключаюць Рыманаву геаметрыю як агульны прыклад. Гэта фармулёўка таксама падыходзіць для еўклідавай прасторы пры ўжыванні крывалінейных каардынат. Напрыклад, для палярных каардынат:
Вектарны здабытак[правіць | правіць зыходнік]

Тэарэма Піфагора звязвае два выразы велічыні вектарнага здабытку. Адзін з падыходаў да вызначэння вектарнага здабытку патрабуе, каб ён задавальняў ураўненні:[29]
у гэтай формуле выкарыстоўваецца скалярны здабытак. Правы бок ўраўненні называецца дэтэрмінант Грама для a і b, што роўна плошчы паралелаграма, ўтворанага гэтымі двума вектарамі. Зыходзячы з гэтага патрабавання, а таксама патрабавання аб перпендыкулярнасці вектарнага здабытку да яго складнікаў a і b вынікае, што, за выключэннем трывіяльных выпадкаў з 0- і 1-мернай прасторы, вектарны здабытак вызначаны толькі ў трох і сямі вымярэннях[30]. Выкарыстоўваем вызначэнне вугла ў n-мернай прасторы:[31]
гэта ўласцівасць вектарнага здабытку дае яго велічыню ў такім выглядзе:
Праз фундаментальную трыганаметрычную тоеснасць Піфагора[32] атрымліваем іншую форму запісу яго велічыні:
[32] Альтэрнатыўны падыход да вызначэння вектарнага здабытку выкарыстоўвае выраз для яго велічыні. Тады, разважаючы ў зваротным парадку, атрымліваем сувязь са скалярных здабыткам:
Тэорыя лікаў[правіць | правіць зыходнік]
Піфагоравай тройкай называецца набор з трох натуральных лікаў якія задавальняюць наступнаму аднароднаму квадратнаму ўраўненні:
Фармулёўка «Вялікай тэарэмы Ферма» аналагічная задачы знаходжання піфагоравых троек для ступені больш за 2.
Згадкі ў мастацкай літаратуры[правіць | правіць зыходнік]
Тэарэма Піфагора згадваецца ў аповесці Яўгена Вялцістава «Электронік — хлопчык з валізкі», дзе Электронік ў ролі Сыраежкіна на ўроку матэматыкі ў школе сцвярджае, што можа даказаць тэарэму Піфагора дваццаццю пяццю спосабамі і прыводзіць некаторыя з іх, чым дзівіць клас і настаўніка матэматыкі Таратара.
Гл. таксама[правіць | правіць зыходнік]
Крыніцы[правіць | правіць зыходнік]
- ↑ Наука, техническая и военная мысль, здравоохранение и образование // Духовная культура Китая: энциклопедия в 5 томах / М. Л. Титаренко. — М.: Восточная литература РАН, 2009. — Т. 5. — С. 939-941. — 1055 с. — ISBN 9785020184299.
- ↑ History topic: Pythagoras’s theorem in Babylonian mathematics Архівавана 6 чэрвеня 2011.
- ↑ (Euclid 1956, p. 351) С. 351
- ↑ (Heath 1921, Vol I, p. 144)
- ↑ Обсуждение исторических фактов приведено в (Euclid 1956, p. 351) С. 351
- ↑ Kurt Von Fritz (April 1945). "The Discovery of Incommensurability by Hippasus of Metapontum". The Annals of Mathematics, Second Series. Annals of Mathematics. 46 (2): 242–264. JSTOR 1969021.
- ↑ Льюис Кэррол, «История с узелками», М., Мир, 1985, с. 7
- ↑
Asger Aaboe (1997). Episodes from the early history of mathematics. Mathematical Association of America. p. 51. ISBN 0883856131.
...it is not until Euclid that we find a logical sequence of general theorems with proper proofs.
- ↑ Pythagorean Proposition, by Elisha Scott Loomis
- ↑ Euclid’s Elements: Book VI, Proposition VI 31: «In right-angled triangles the figure on the side subtending the right angle is equal to the similar and similarly described figures on the sides containing the right angle.»
- ↑ Lawrence S. Leff (2005-05-01). cited work. Barron's Educational Series. p. 326. ISBN 0764128922.
- ↑ Howard Whitley Eves (1983). "§4.8:...generalization of Pythagorean theorem". Great moments in mathematics (before 1650). Mathematical Association of America. p. 41. ISBN 0883853108.
- ↑ Tâbit ibn Qorra (full name Thābit ibn Qurra ibn Marwan Al-Ṣābiʾ al-Ḥarrānī) (826—901 AD) was a physician living in Baghdad who wrote extensively on Euclid’s Elements and other mathematical subjects.
- ↑
Aydin Sayili (March 1960). "Thâbit ibn Qurra's Generalization of the Pythagorean Theorem". Isis. 51 (1): 35–37. doi:10.1086/348837. JSTOR 227603.
{{cite journal}}: Папярэджанні CS1: date і year (link) - ↑ Judith D. Sally, Paul Sally (2007-12-21). "Exercise 2.10 (ii)". Cited work. p. 62. ISBN 0821844032.
- ↑ а б For the details of such a construction, see George Jennings (1997). "Figure 1.32: The generalized Pythagorean theorem". Modern geometry with applications: with 150 figures (3rd ed.). Springer. p. 23. ISBN 038794222X.
- ↑ Arlen Brown, Carl M. Pearcy (1995). "Item C: Norm for an arbitrary n-tuple ...". An introduction to analysis. Springer. p. 124. ISBN 0387943692. See also pages 47-50.
- ↑
Alfred Gray, Elsa Abbena, Simon Salamon (2006). Modern differential geometry of curves and surfaces with Mathematica (3rd ed.). CRC Press. p. 194. ISBN 1584884487.
{{cite book}}: Папярэджанні CS1: розныя назвы: authors list (link) - ↑ Rajendra Bhatia (1997). Matrix analysis. Springer. p. 21. ISBN 0387948465.
- ↑ Stephen W. Hawking (2005). cited work. p. 4. ISBN 0762419229.
- ↑
Eric W. Weisstein (2003). CRC concise encyclopedia of mathematics (2nd ed.). p. 2147. ISBN 1584883472.
The parallel postulate is equivalent to the Equidistance postulate, Playfair axiom, Proclus axiom, the Triangle postulate and the Pythagorean theorem.
- ↑
Alexander R. Pruss (2006). The principle of sufficient reason: a reassessment. Cambridge University Press. p. 11. ISBN 052185959X.
We could include...the parallel postulate and derive the Pythagorean theorem. Or we could instead make the Pythagorean theorem among the other axioms and derive the parallel postulate.
- ↑ Victor Pambuccian (December 2010). "Maria Teresa Calapso's Hyperbolic Pythagorean Theorem". The Mathematical Intelligencer. 32 (4): 2. doi:10.1007/s00283-010-9169-0.
- ↑ Barrett O'Neill (2006). "Exercise 4". Elementary differential geometry (2nd ed.). Academic Press. p. 441. ISBN 0120887355.
- ↑ Saul Stahl (1993). "Theorem 8.3". The Poincaré half-plane: a gateway to modern geometry. Jones & Bartlett Learning. p. 122. ISBN 086720298X.
- ↑ Микиша А. М., Орлов В. Б. «Толковый математический словарь. Основные термины.», М. «Русский язык», 1989 г.
- ↑ Jane Gilman (1995). "Hyperbolic triangles". Two-generator discrete subgroups of PSL(2,R). American Mathematical Society Bookstore. ISBN 0821803611.
- ↑ Tai L. Chow (2000). Mathematical methods for physicists: a concise introduction. Cambridge University Press. p. 52. ISBN 0521655447.(недаступная спасылка)
- ↑
WS Massey (December 1983). "Cross products of vectors in higher dimensional Euclidean spaces". The American Mathematical Monthly. Mathematical Association of America. 90 (10): 697–701. doi:10.2307/2323537. JSTOR 2323537.
{{cite journal}}: Папярэджанні CS1: date і year (link) - ↑ Although a cross-product involving n − 1 vectors can be found in n dimensions, a cross-product involving only two vectors can be found only in 3 dimensions and in 7 dimensions. See Pertti Lounesto (2001). "§7.4 Cross product of two vectors". Clifford algebras and spinors (2nd ed.). Cambridge University Press. p. 96. ISBN 0521005515.(недаступная спасылка)
- ↑ Francis Begnaud Hildebrand (1992). Methods of applied mathematics (Reprint of Prentice-Hall 1965 2nd ed.). Courier Dover Publications. p. 24. ISBN 0486670023.
- ↑ а б Lawrence S. Leff (2005). PreCalculus the Easy Way (7th ed.). Barron's Educational Series. p. 296. ISBN 0764128922.
Літаратура[правіць | правіць зыходнік]
- Скопец З. А. Геометрические миниатюры. — М., 1990.
- Еленьский Щ. По следам Пифагора. — М., 1961.
- Ван-дер-Варден Б. Л. Пробуждающаяся наука. Математика Древнего Египта, Вавилона и Греции. — М., 1959.
- Глейзер Г. И. История математики в школе. — М., 1982.
- Euclid (1956). The Thirteen Books of Euclid's Elements, Translated from the Text of Heiberg, with Introduction and Commentary. Vol. 1 (Books I and II). Перакладчык Heath, Thomas L. (Reprint of 2nd (1925) ed.). Dover. On-line text at archive.org
- Heath, Sir Thomas (1921). "The 'Theorem of Pythagoras'". A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) ed.). Clarendon Press, Oxford. pp. 144 ff. ISBN 0-486-24073-8.
Спасылкі[правіць | правіць зыходнік]
- В. Литцман, «Теорема Пифагора» — М., 1960.
- Сайт о теореме Пифагора с большим числом доказательств, материал взят из книги В. Литцмана, большое число чертежей представлено в виде отдельных графических файлов.
- Теорема Пифагора и пифагоровы тройки Архівавана 3 сакавіка 2016. глава из книги Д. В. Аносова «Взгляд на математику и нечто из неё»
- История теоремы Пифагора
- О теореме Пифагора и способах её доказательства Архівавана 17 снежня 2007. Г. Глейзер, академик РАО, Москва
- Ролик серии «Математические этюды», посвящённый теореме Пифагора (для компьютера, iPhone, iPad)
- Тэарэма Піфагора на WolframMathWorld (англ.)
- Cut-The-Knot, секцыя, прысвечаная тэарэме Піфагора, каля 70 доказаў і шырокая дадатковая інфармацыя (англ.)









































![{\displaystyle 1-\left({\frac {c}{R}}\right)^{2}=\left[1-\left({\frac {a}{R}}\right)^{2}\right]\left[1-\left({\frac {b}{R}}\right)^{2}\right]+o(a^{2}+b^{2})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34d59bfbc6dad385c428d0ab5a79bcf628592dd4)













