Закон адваротных квадратаў

Лініі абазначаюць паток, выходны ад крыніцы. Агульная колькасць ліній патоку залежыць ад магутнасці крыніцы і застаецца нязменнай з павелічэннем адлегласці ад яе. Больш высокая шчыльнасць ліній (колькасць ліній на адзінку плошчы) азначае больш моцнае поле. Шчыльнасць ліній патоку назад прапарцыянальная квадрату адлегласці ад крыніцы, так як плошча паверхні сферы расце прапарцыянальна квадрату радыусу. Такім чынам, сіла поля адваротна прапарцыянальная квадрату адлегласці ад крыніцы.

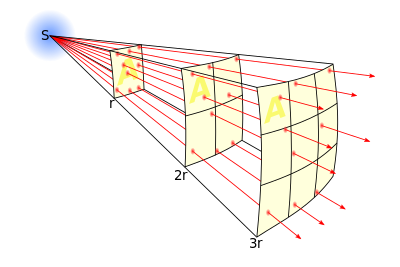
У фізіцы закон адваротных квадратаў — гэта закон, які сцвярджае, што значэнне некаторай фізічнай велічыні ў дадзенай кропцы прасторы адваротна прапарцыянальна квадрату адлегласці ад крыніцы поля, якое характарызуе гэтая фізічная велічыня.

Абгрунтаванне

Закон адваротных квадратаў у агульным выпадку выкарыстоўваецца і ў дачыненні, калі лініі дзеяння некаторай сілы, або энергія ці іншая велічыня, якая захоўвае поўнае значэнне, разыходзіцца (распаўсюджваецца) у радыяльным кірунку ад крыніцы. Па меры таго, як плошча сферы (якая вызначаецца па формуле $4\pi r^{2}$) расце прапарцыянальна квадрату адлегласці ад крыніцы (радыусу сферы), і як выпушчанае выпраменьванне выдаляецца ўсё далей ад крыніцы, гэта выпраменьванне павінна праходзіць праз паверхню, плошча якой расце прапарцыянальна квадрату адлегласці ад крыніцы. Такім чынам, інтэнсіўнасць выпраменьвання, якое праходзіць праз адну і тую ж плошчу, адваротна прапарцыянальная квадрату адлегласці ад крыніцы.

Праявы

Гравітацыя

Гравітацыя — гэта ўзаемадзеянне паміж двума аб'ектамі, якія валодаюць масамі. Такія аб'екты падпарадкоўваюцца закону сусветнага прыцягнення :

Сілы гравітацыйнага ўзаемадзеяння паміж двума кропкавымі масамі прама прапарцыянальныя здабытку гэтых мас, і адваротна прапарцыянальныя квадрату адлегласці паміж імі. Гэтыя сілы заўсёды дзейнічаюць і накіраваны ўздоўж прамой, якая злучае гэтыя кропкавыя масы.

Калі размеркаванне мас у пэўным матэрыяльным некропкавым аб'екце валодае сферычнай сіметрыяй, то такі аб'ект можа разглядацца як кропкавая маса (матэрыяльны пункт).

Аднак, калі мы хочам разлічыць сілу ўзаемадзеяння паміж масіўнымі целамі, мы павінны скласці вектарна сілы ўзаемадзеяння паміж усімі парамі кропкавых мас, якія ўтвараюць дадзенае масіўнае цела, і выніковае ўзаемадзеянне можа не падпарадкоўвацца закону адваротных квадратаў. У той жа час, калі адлегласці паміж двума масіўнымі аб'ектамі вельмі вялікія ў параўнанні з памерамі гэтых аб'ектаў, то мэтазгодна разглядаць гэтыя аб'екты як матэрыяльныя кропкі пры разліку сіл гравітацыйнага ўзаемадзеяння паміж імі.

Як закон адваротных квадратаў закон сусветнага прыцягнення быў сфармуляваны ў 1645 Ісмаэлям Буйё (Буліяльдам). Гэта адрознівалася ад здагадкі Ёгана Кеплера аб адваротна прапарцыянальнай залежнасці ад адлегласці. Але Буліяльд не прызнаваў справядлівасць ні другога і трэцяга законаў Кеплера, ні рашэнні Хрысціяна Гюйгенса для руху па акружнасці. Буляальд лічыў, што сонца прыцягваецца у афеліі і адштурхваецца ў пэрыгеліі.

Роберт Гук і Джавані Альфонса Барэлі у 1666 г. падрабязна апісалі гравітацыйную сілу як прыцягальную сілу. У лекцыі ў 1670 Гук патлумачыў, што гравітацыя ўласцівая «ўсім нябесным целам» і ўвёў прынцып, які сцвярджае, што сіла гравітацыі меншае з адлегласцю. Да 1679 Гук прыйшоў да высновы, што гравітацыя мае адваротна прапарцыянальную залежнасць квадрату адлегласці. Ён паведаміў гэта ў лісце да Ісаака Ньютана. Гук быў досыць рэзкі, нягледзячы нават на тое, што ў сваёй працы «Пачаткі» Ньютан прызнаў, што Гук разам з Рэнам і Галеем незалежна адзін ад аднаго ўжывалі закон адваротных квадратаў для сонечнай сістэмы, таксама як аддаў даніну павагі Буліяльду.

Электрастатыка

Сіла прыцягнення або адштурхвання, якая дзейнічае паміж двума зараджанымі часціцамі, у даданне да прама прапарцыянальнай залежнасці ад здабытку зарадаў, з'яўляецца адваротна прапарцыянальнай квадрату адлегласці паміж імі. Гэта зацвярджэнне вядома пад назвай закона Кулона.

Святло і іншыя віды электрамагнітнага выпраменьвання

Інтэнсіўнасць святла (гэта значыць, энергія, якая прыходзіцца на адзінку плошчы ў адзінку часу) або іншых лінейных хваль, выходных ад кропкавай крыніцы адваротна прапарцыянальная квадрату адлегласці ад крыніцы. Гэта значыць, напрыклад, што аб'ект, перамешчаны на адлегласць у 2 разы большую ад крыніцы, атрымлівае толькі чвэрць той магутнасці, якую ён атрымліваў у першапачатковым становішчы.

Напрыклад, інтэнсіўнасць сонечных прамянёў складае 9140 Вт на квадратны метр на арбіце Меркурыя, але толькі 1370 Вт на арбіце Зямлі (на тую ж плошчу) — трохразовае павелічэнне адлегласці цягне дзевяціразовае памяншэнне інтэнсіўнасці сонечных прамянёў.

Варта адзначыць, што ў адрозненне ад інтэнсіўнасці і ад поля ў статычным выпадку, амплітуда напружанасці электрычнага поля і магнітнай індукцыі ў электрамагнітнай хвалі ад кропкавай крыніцы падае адваротна прапарцыянальна першай ступені адлегласці :

$E_{a},B_{a}\propto {1 \over r}$

Фатографы і тэатральныя майстры па свеце выкарыстоўваюць закон адваротных квадратаў для выбару аптымальнага месца становішча асвятляльных прыбораў.

Закон адваротных квадратаў можа быць ужыты толькі для кропкавых крыніц святла; найбольш распаўсюджаныя ў памяшканнях цыліндрычныя лямпы дзённага святла не з'яўляюцца кропкавымі крыніцамі, і таму да іх нельга ўжываць закон адваротных квадратаў, у адрозненне ад большасці іншых крыніц штучнага выпраменьвання.

Закон адваротных квадратаў мае некаторае значэнне ў дыягнастычнай рэнтгенаграфіі і радыяцыйнай тэрапіі для разліку дозы апраменьвання. Аднак гэтая прапарцыянальнасць не выконваецца ў практычных выпадках, нягледзячы нават на тое, што памеры крыніц апраменьвання нашмат менш адлегласцей да аб'екта апрамянення.

Формулы закона зваротных квадратаў у рэнтгенаграфіі маюць выгляд:

${\frac {I_{1}}{I_{2}}}=\left({\frac {r_{2}}{r_{1}}}\right)^{2}$

дзе

I — інтэнсіўнасць,

r — адлегласць (радыус).

Прыкладанні ў тэорыі поля

Для бязвіхурнага вектарнага поля ў трохмернай прасторы закон адваротных квадратаў звязаны з тым уласцівасцю, што дывергенцыя звяртаецца ў нуль звонку крыніцы.