Паралелаграм

Паралелагра́м (ад грэц. parallelos — паралельны і gramme — лінія) — гэта чатырохвугольнік, у якога процілеглыя бакі парамі паралельныя, г. зн. ляжаць на паралельных прамых. Прамавугольнік, ромб і квадрат з'яўляюцца асобнымі выпадкамі паралелаграма.

Асаблівасці

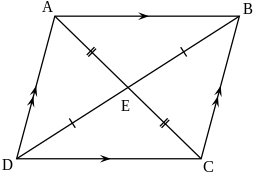
• Процілеглыя бакі паралелаграма роўныя

  $|AB| = |CD|$, $|AD| = |BC|$.

• Процілеглыя вуглы паралелаграма роўныя

  $\angle A = \angle C, \angle B = \angle D.$

• Дыяганалі паралелаграма перасякаюцца і пунктам скрыжавання палавіняцца

  $|AO| = |OC|$, $|BO| = |OD|$.

• Сума вуглоў, прылеглых да аднаго боку, роўная 180°.
• Сума квадратаў дыяганаляў паралелаграма роўная суме квадратаў яго чатырох бакоў

  $|AC|^2 + |BD|^2 = |AB|^2 + |BC|^2 + |CD|^2 + |AD|^2.$

Доказы  

Правядучы дыяганаль BD, мы атрымаем два трохвугольніка ABD і BCD, якія роўныя, бо адзін бок у іх агульны, а адпаведныя вуглы пры боку BD роўныя як накрыж ляжалыя пры паралельных прамых AB

Прыкметы паралелаграма

Чатырохвугольнік ABCD з'яўляецца паралелаграмам, калі выконваецца адна з наступных умоў:

1. Процілеглыя бакі парамі роўныя (|AB| = |CD|, |AD| = |BC|).
2. Процілеглыя вуглы парамі роўныя (∠A = ∠C, ∠B = ∠D).
3. Два процілеглыя бакі роўныя і паралельныя (|AB| = |CD|, AB || CD).
4. Дыяганалі дзеляцца ў пункце іх скрыжавання напалову (|AO| = |OC|, |BO| = |OD|).

Доказы  

• Хай чатырохвугольнік ABCD такі што:

Плошча

Плошчу паралелаграма можна знайсці па наступных формулах:

$S_{ABCD}=|AD|\cdot h_{AD}=|AB|\cdot |AD| \sin \alpha = \frac{1}{2} |AC|\cdot|BD|\sin \beta .$

Гл. таксама

• Трапецыя
• Прамавугольнік
• Ромб
• Дэльтоід