Гама-функцыя

Абсалютная велічыня гама-функцыі на камплекснай плоскасці

Гама-функцыя (або Эйлераў інтэграл другога роду) — матэматычная функцыя, якая пашырае паняцце фактарыяла на поле камплексных лікаў. Звычайна абазначаецца грэчаскай літарай гама Γ(z).

Для натуральных n справядліва роўнасць:

$\Gamma (n)=(n-1)!$

Гама-функцыя вызначана для ўсіх камплексных лікаў, за выключэннем адмоўных цэлых і нуля. Для камплексных лікаў з дадатнай рэчаіснай часткай, функцыя вызначаецца з дапамогаю збежнага неўласцівага інтэграла:

$\Gamma (t)=\int \limits _{0}^{\infty }x^{t-1}e^{-x}\,dx.$

Гэту інтэгральную функцыю можна аналітычна працягнуць на ўсю камплексную плоскасць, за выключэннем недадатных цэлых лікаў (дзе функцыя мае простыя полюсы). Атрыманая ў выніку мераморфная функцыя і называецца гама-функцыяй.

Была ўведзена Леанардам Эйлерам, а сваім абазначэннем гама-функцыя абавязана Лежандру.

Азначэнні

Графік гама-функцыі рэчаіснай зменнай

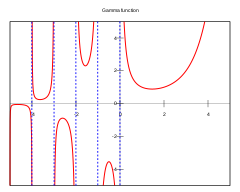
Інтэгральнае азначэнне

Калі рэчаісная частка камплекснага ліку $z$ дадатная, то Гама-функцыя вызначаецца праз інтэграл

$~\Gamma (z)=\int \limits _{0}^{+\infty }t^{{\mathrm {z} }-1}e^{-t}\,dt,\quad z\in \mathbb {C} :\mathrm {Re} (z)>0$

На ўсю камплексную плоскасць функцыя аналітычна працягваецца праз тоеснасць

$~\Gamma (z+1)=z\Gamma (z).$

Існуе непасрэдны аналітычны працяг зыходнай формулы на ўсю камплексную плоскасць, т. зв. інтэграл Рымана-Ханкеля

$~\Gamma (z)={\frac {1}{e^{i2\pi {\mathrm {z} }}-1}}\int \limits _{L}\!t^{{\mathrm {z} }-1}e^{-t}\,dt,\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \}.$

дзе контур $L$ — любы контур на камплекснай плоскасці, які абходзіць пункт $t=0$ супраць гадзіннікавай стрэлкі, і канцы якога ідуць на бесканечнасць уздоўж дадатнай рэчаіснае восі.

Наступныя выразы з'яўляюцца альтэрнатыўнымі азначэннямі Гама-функцыі.

Азначэнне па Гаусу

Яно вернае для ўсіх камплексных $z$, за выключэннем 0 і адмоўных цэлых лікаў

$\Gamma (z)=\lim \limits _{n\to \infty }{\frac {n!\,n^{z}}{z(z+1)(z+2)\cdots (z+n)}},\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \}.$

Азначэнне па Эйлеру

$\Gamma (z)={\frac {1}{z}}\left(\prod \limits _{n=1}^{\infty }{\left(1+{\frac {1}{n}}\right)}^{z}{\left(1+{\frac {z}{n}}\right)}^{-1}\right)={\frac {1}{z}}\prod _{n=1}^{\infty }{\frac {\left(1+{\frac {1}{n}}\right)^{\mathrm {z} }}{1+{\frac {\mathrm {z} }{n}}}},\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \}.$

Азначэнне па Веерштрасу

$\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{z/n},\quad z\in \mathbb {C} \setminus \{0,-1,-2,\ldots \},$

дзе $\gamma =\lim \limits _{n\to \infty }\left(\sum \limits _{k=1}^{n}{\frac {1}{k}}-\ln {n}\right)\approx 0,57722$ — пастаянная Эйлера — Маскероні.

Заўвагі

• Вышэйпрыведзены інтэграл збягаецца абсалютна, калі рэчаісная частка камплекснага ліку $z$ дадатна.
• Прымяняючы інтэграванне па частках, можна паказаць, што тоеснасць

  $\Gamma (z+1)=z\Gamma (z)$

справядліва для падынтэгральнага выразу.

• Паколькі $\Gamma (1)=1$, для ўсіх натуральных лікаў $n$

$\Gamma (n+1)=n\cdot \Gamma (n)=\ldots =n!\cdot \Gamma (1)=n!$

• $\Gamma (z)$ з'яўляецца мераморфнаю на камплекснай плоскасці і мае полюсы ў пунктах $z=0,\;-1,\;-2,\;-3,\;\ldots$

Звязаныя азначэнні

• Калі-нікалі выкарыстоўваецца альтэрнатыўны запіс, так званая пі-функцыя, якая звязана з гама-функцыяй наступным чынам:

  $\Pi (z)=\Gamma (z+1)=z\Gamma (z).$

• У інтэграле з азначэння гама-функцыі, межы інтэгравання нязменныя. Разглядаюць таксама няпоўную гама-функцыю, якую вызначаюць падобным інтэгралам са зменнай верхняй ці ніжняй мяжою інтэгравання. Вылучаюць верхнюю няпоўную гама-функцыю, якую часта абазначаюць як гама-функцыю ад двух аргументаў:

$\Gamma (a,z)=\int \limits _{\mathrm {z} }^{\infty }{t^{a-1}e^{-t}\,dt},$

і ніжнюю няпоўную гама-функцыю, якую таксама абазначаюць малой літарай «гама»:

$\gamma (a,z)=\int \limits _{0}^{\mathrm {z} }{t^{a-1}e^{-t}\,dt}.$

Уласцівасці

Графік модуля гама-функцыі на камплекснай плоскасці.

• Формула дапаўнення Эйлера:

  $\Gamma (1-z)\Gamma (z)={\pi \over \sin \pi z}.$

• З яе вынікае формула памнажэння Гауса:

  $\Gamma (z)\Gamma \left(z+{\frac {1}{n}}\right)\ldots \Gamma \left(z+{\frac {n-1}{n}}\right)=n^{{\frac {1}{2}}-nz}\cdot (2\pi )^{\frac {n-1}{2}}\Gamma (nz),$

• якую пры n=2 называюць формулай падваення Лежандра:

  $\Gamma (z)\;\Gamma \left(z+{\frac {1}{2}}\right)=2^{1-2z}\;{\sqrt {\pi }}\;\Gamma (2z).\,\!$

• Гама-функцыя мае полюс у $z=-n$ для любога натуральнага $n$ і нуля; вылік у гэтым пункце задаецца так:

  $\operatorname {Res} _{z=-n}\Gamma (z)={\frac {(-1)^{n}}{n!}}.$

• Наступнае прадстаўленне гама-функцыі ў выглядзе бесканечнага здабытку, як паказаў Веерштрас, верна для ўсіх камплексных $z$, акрамя недадатных цэлых лікаў:

  $\Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{k=1}^{\infty }\left(1+{\frac {z}{k}}\right)^{-1}e^{z/k},$

дзе $\gamma$ — пастаянная Эйлера — Маскероні.

• Важная ўласцівасць, якая вынікае з гранічнага азначэння:

  ${\overline {\Gamma (z)}}=\Gamma ({\overline {z}})$.

• Гама-функцыя бесканечна дыферэнцавальная, і

  $\Gamma ^{\prime }(x)=\psi (x)\Gamma (x),$

дзе $\psi (x)$ часта называюць «псі-функцыяй», ці дыгама-функцыяй.

• Гама-функцыя і бэта-функцыя звязаны наступнымі суадносінамі:

  $\mathrm {B} (x,y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}}.$

Асобныя значэнні

• Найбольш вядомыя значэнні гама-функцыі ад няцэлага аргумента:

  $\Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}.$

  $\Gamma \left({\frac {1}{4}}\right)={\sqrt {\frac {(2\pi )^{3/2}}{AGM({\sqrt {2}},1)}}},$

  дзе AGM(x, y) — сярэдняе арыфметыка-геаметрычнае лікаў x і y.

  $\Gamma \left({\frac {3}{2}}\right)={\frac {\sqrt {\pi }}{2}}.$

  $\Gamma \left({\frac {1}{2}}+n\right)={(2n)! \over 4^{n}n!}{\sqrt {\pi }}={\frac {(2n-1)!!}{2^{n}}}\,{\sqrt {\pi }}={\sqrt {\pi }}\cdot \left[{n-{\frac {1}{2}} \choose n}n!\right]$

  $\Gamma \left({\frac {1}{2}}-n\right)={(-4)^{n}n! \over (2n)!}{\sqrt {\pi }}={\frac {(-2)^{n}}{(2n-1)!!}}\,{\sqrt {\pi }}={\sqrt {\pi }}/\left[{-{\frac {1}{2}} \choose n}n!\right]$

Гл. таксама

• Спіс аб'ектаў, названых у гонар Леанарда Эйлера
• K-функцыя
• G-функцыя Барнса
• Бэта-функцыя
• Гама-размеркаванне
• Няпоўная гама-функцыя
• Формула Стырлінга

Літаратура

• Купцов Л. П. Гамма-функция // Математическая энциклопедия / И. М. Виноградов (гл. ред.). — М.: Советская энциклопедия. — Т. 1.

Спасылкі

• Weisstein, Eric W.. Gamma Function (нявызн.). MathWorld.