Дыяграмы Фейнмана
Дыяграмы Фейнмана — наглядны і эфектыўны спосаб апісання ўзаемадзеяння ў квантавай тэорыі поля (КТП).
Метад прапанаваны Рычардам Фейнманам ў 1949 для пабудовы амплітуд рассейвання і ўзаемнага ператварэння элементарных часціц у рамках тэорыі ўзбурэнняў, калі з поўнага (эфектыўнага) лагранжыяна сістэмы палёў вылучаецца неўзбураная частка (свабодны лагранжыян) , квадратычная па палях, а астатняя частка (лагранжыян узаемадзеяння) трактуецца як узбурэнне. Найбольш наглядную інтэрпрэтацыю дыяграмы Фейнмана набываюць у метадзе інтэгралаў па траекторыях.

Дыяграмы Фейнмана шырока выкарыстоўваюцца для аналізу аналітычных уласцівасцей амплітуд рассейвання, у прыватнасці для даследавання іх асаблівасцей (сінгулярнасці). Часам гэта дазваляе з усяе сукупнасці дыяграм, якія адпавядаюць гэтаму працэсу, вылучыць некаторую падсукупнасць, якая ўносіць асноўны ўклад.
Метад дыяграм Фейнмана паспяхова прымяняецца таксама ў квантавай тэорыі многіх часціц, у прыватнасці для апісання кандэнсаваных цел і ядзерных рэакцый.
Апісанне метаду[правіць | правіць зыходнік]
Складовымі элементамі дыяграмы Фейнмана з'яўляюцца вяршыні, унутраныя і знешнія лініі. Кожная з ліній далучаецца да якіх-небудзь вяршынь: унутраная да двух, а знешняя да адной. Набор вяршынь вызначаецца структурай , а набор знешніх і ўнутраных ліній — структурай . Кожнаму маному па палях у адпавядае пэўны тып вяршынь, а кожнаму тыпу поля ў пэўны тып ліній. Калі поле нейтральнае (адпаведная часціца супадае са сваёй антычасціцай), то лінія лічыцца ненакіраванай, у адваротным выпадку лінія накіраваная і на дыяграме забяспечваецца стрэлкай.
Існуюць так званыя правілы Фейнмана, якія супастаўляюць кожнаму элементу дыяграмы Фейнмана пэўныя матэматычныя аб'екты (велічыні і аперацыі), так што па дыяграме Фейнмана можна адназначна пабудаваць аналітычны выраз, які дае ўклад у амплітуду рассейвання квантованых палёў. Разам з тым дыяграмы Фейнмана дазваляюць такому ўкладу даць наглядную класічную інтэрпрэтацыю ў выглядзе рада паслядоўных лакальных ператварэнняў часціц. Кожнаму асобныму ператварэнню адпавядае вяршыня, унутраным лініям — распаўсюджванне прамежкавай часціцы ад аднаго акта ператварэння да іншага (прапагатар часціцы), вонкавым лініям — хвалевыя функцыі пачатковых і канчатковых часціц, якія ўдзельнічаюць у працэсе.
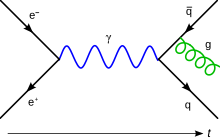
У якасці прыкладу разгледзім дыяграмы Фейнмана ў квантавай электрадынаміцы (КЭД), якая апісвае ўзаемадзеянне электронаў, пазітронаў і фатонаў паміж сабой. У КЭД ёсць усяго адзін тып вяршынь (рыс. 1) і два тыпы ліній (рыс. 2). Ненакіраваная хвалістая лінія адносіцца да фатона, а накіраваная прамая — да электрона і пазітрона.
У апошнім выпадку распаўсюджванню асноўнай часціцы (электрона) адпавядае рух уздоўж лініі па стрэлцы, а распаўсюджванню антычасціцы (пазітрона) — рух супраць стрэлкі.
Кожная дыяграма Фейнмана мае некалькі інтэрпрэтацый у залежнасці ад кірунку руху ўздоўж ліній гэтай дыяграмы. Так, для дыяграмы Фейнмана, намаляванай на рыс. 3, дапушчальныя наступныя варыянты.
- Рух па лініях злева направа — рассейванне фатона на электроне. У вяршыні 1 пачатковы электрон паглынае пачатковы фатон, пры гэтым утвараецца прамежкавы электрон, які распаўсюджваецца ад вяршыні 1 да вяршыні 2. Тут ён выпраменьвае канчатковы фатон і ператвараецца ў канчатковы электрон. Вынікам працэсу з'яўляецца пераразмеркаванне 4-імпульсу (энергіі і імпульсу) паміж электронам і фатонам.
- Рух па лініях справа налева — рассейванне фатона на пазітроне.
- Рух знізу ўверх — анігіляцыі электрона і пазітрона з ператварэннем іх у два фатона.
- Рух зверху ўніз — нараджэнне электрон-пазітроннай пары пры сутыкненні двух фатонаў.
Гл. таксама[правіць | правіць зыходнік]
Літаратура[правіць | правіць зыходнік]
- Р. Фейнман. КЭД — странная теория света и вещества. (Библиотечка «Квант», вып. 66) М., Наука, 1988 Архівавана 18 снежня 2005.
Спасылкі[правіць | правіць зыходнік]
У іншым моўным раздзеле ёсць больш поўны артыкул Диаграммы Фейнмана(руск.) |





