Лагарыфм

Графік двайковага лагарыфма

Лагары́фм ліку x па аснове b (от грэч. λόγος — «слова», «дачыненне» и ἀριθμός — «лік») — такое значэнне ступені, у якую трэба ўзвесці лік b, называны асно́вай, каб атрымаць значэнне x. Абазначэнне $\log_b a$ чытаецца як "лагарыфм $a$ па аснове $b$".

З азначэння вынікае, што знаходжанне $x = \log_b a$ раўназначнае развязанню раўнання $b^x=a$. Напрыклад, лагарыфм 1000 па аснове 10 роўны 3, бо 1000 з'яўляецца 10 у ступені 3: 1000 = 10·10·10 = 10³.

Вылічэнне лагарыфма называецца лагарыфмава́ннем.

Лагарыфмы маюць цікавыя ўласці́васці, якія дазваляюць спрашчаць працаёмкія вылічэнні. Пры пераходзе «ў свет лагарыфмаў» множанне замяняецца на значна прасцейшае складанне, дзяленне - на адыманне, а ўзвядзенне ў ступень і здабыванне кораня ператвараюцца адпаведна ў множанне і дзяленне на паказнік ступені. Лаплас казаў, што вынаходніцтва лагарыфмаў, «скараціўшы працу астранома, падвоіла яго жыццё». У дастасаваннях аснова $b$ лагарыфма і лагарыфмаваны лік (аргумент лагарыфма) звычайна рэчаісныя. Тым не менш, існуе шэраг праблем (у тым ліку і прыкладных), дзе карысным аказваецца так званы камплексны лагарыфм.

Азначэнне лагарыфмаў і табліцу іх значэнняў (для трыганаметрычных функцый) упершыню надрукаваў у 1614 годзе шатландскі матэматык Джон Нэпер. Лагарыфмічныя табліцы, пашыраныя і ўдакладненыя іншымі матэматыкамі, паўсюдна выкарыстоўваліся ў навуковых і інжынерных разліках больш за тры стагоддзі, пакуль не з'явіліся электронныя вылічальныя машыны.

З цягам часу высветлілася, што лагарыфмічная функцыя $y=\log_b x$ незаменная і ў шмат якіх іншых галінах чалавечай дзейнасці: развязанні дыферэнцыяльных раўнанняў, вымярэнні фізічных велічынь (напрыклад, частаты і магутнасці гуку), набліжанні розных залежнасцей, тэорыі інфармацыі, тэорыі імавернасцей і г. д. Гэта функцыя ўваходзіць у лік элементарных, яна ёсць адваротнай да паказнікавай функцыі. Часцей за ўсё выкарыстоўваюцца рэчаісныя лагарыфмы па аснове e (натуральны), 10 (дзесятковы) і 2 (двайковы).

Рэчаісны лагарыфм

Лагарыфм $x=\log_b a$ па азначэнні ёсць развязкам раўнання $b^x=a$. Выпадак $b=1$ не дужа цікавы, бо пры $a \ne 1$ гэта раўнанне не мае развязка, а пры $a=1$ любы лік з'яўляецца развязкам; у абодвух выпадках лагарыфм не вызначаны. Гэтак жа прыходзім да высновы, што лагарыфм не існуе пры нулявым і адмоўным $b$; акрамя таго, значэнне паказнікавай функцыі $b^x$ заўсёды дадатнае, таму варта выключыць і выпадак адмоўнага $a$. Канчаткова атрымоўваем:

Рэчаісны лагарыфм $\log_b a$ вызначаны пры $b>0, b \ne 1, a>0$.

Як вядома, паказнікавая функцыя $y=b^x$ (пры выкананні вышэйазначаных умоў на $b$) вызначана, манатонная і кожнае значэнне прымае толькі адзін раз, прычым абсяг яе значэнняў утрымлівае ўсе дадатныя рэчаісныя лікі. Адсюль вынікае, што значэнне рэчаіснага лагарыфма дадатнага ліку заўсёды вызначана і адзінае.

Найбольш шырокі ўжытак і шматлікія дастасаванні маюць наступныя віды лагарыфмаў:

• Натуральны: $\ln x$, аснова: лік Ойлера e.
• Дзесятковы: $\lg x$, аснова: лік 10.
• Двайковы: $\log_2 x$ або $\operatorname{lb} x$, аснова: 2. Яны ўжываюцца, напрыклад, у тэорыі інфармацыі, інфарматыцы, у многіх раздзелах дыскрэтнай матэматыкі.

Уласцівасці

Асноўная лагарыфмічная тоеснасць

З азначэння лагарыфма вынікае асноўная лагарыфмічная тоеснасць:

• $a^{\log_a x} = x$

• $\log_a \left(a^x\right) = x$

Выснова: з роўнасці двух рэчаісных лагарыфмаў вынікае раўнасць лагарыфмаваных выразаў. Сапраўды, калі $\log_a b=\log_a c$, то $a^{\log_a b} = a^{\log_a c}$, адкуль, адпаведна асноўнай тоеснасці: $b=c$.

Лагарыфмы адзінкі і ліку, роўнага аснове

• $\log_a 1 = 0$,

• $\log_a a = 1$.

Арыфметычныя ўласцівасці лагарыфма

• Лагарыфм здабытку:

$\log_a(x y) = \log_a (x) + \log_a (y)$

• Лагарыфм дзелі:

$\log_a \left(\frac{x}{y}\right) = \log_a (x) - \log_a (y)$

• Лагарыфм ступені:

$\log_a(x^p) = p \log_a (x)$

• Лагарыфм кораня:

$\log_a \sqrt[p]{x} = \frac{\log_a (x)}{p}$

• Калі аснова лагарыфма ёсць ступенню некаторага выразу:

$\log_{a^k} b = \frac{1}{k} \log_a b$.

Доказ: Гэта тоеснасць атрымліваецца адразу, калі ад лагарыфма па аснове $a^k$ перайсці да лагарыфма па аснове $a$.

Вынікі:

$\log_{\sqrt[n]{a}} b = n \log_a b; \quad \log_{a^k}{b^p} = \frac{p}{k}\log_a{b}; \quad \log_{a^k} b^k = \log_a b$.

• Яшчэ адна карысная тоеснасць:

$c^{\log_a b}=b^{\log_a c}$

Доказ: Каб даказаць яе, заўважым, што лагарыфмы ў левай і правай частках супадаюць па аснове $a$, а тады, згодна з вынікам з асноўнай лагарыфмічнай тоеснасці, левая і правая часткі тоесна роўныя.

Існуе відавочнае абагульненне прыведзеных формул:

$\log_a |x y| = \log_a |x| + \log_a |y|$

$\log_a \left|\frac x y \right| = \log_a |x| - \log_a |y|$

Формула для лагарыфма здабытку без цяжкасцей абагульняецца на адвольную колькасць сумножнікаў:

$\log_a(x_1 x_2 \dots x_n) = \log_a (x_1) + \log_a (x_2) + \dots + \log_a (x_n)$

Апісанымі ўласцівасцямі і тлумачыцца, чаму выкарыстанне лагарыфмаў (да вынаходніцтва калькулятараў) істотна палягчала вылічэнні. Напрыклад, множанне шматзначных лікаў $x, y$ з дапамогай лагарыфмічных табліц адбывалася па наступным алгарытме:

1. Знайсці ў табліцах лагарыфмы лікаў $x, y$.
2. Скласці гэтыя лагарыфмы, атрымаўшы такім чынам (згодна з первай уласцівасцю) лагарыфм здабытку $x \cdot y$.
3. Па лагарыфме здабытку знайсці ў табліцах сам здабытак.

Дзяленне, якое без дапамогі лагарыфмаў істотна больш працаёмкае чым множанне, выконвалася па тым жа алгарытме, толькі з заменай складання лагарыфмаў на адыманне. Гэтак жа спрашчаліся ўзвядзенне ў ступень і здабыванне кораня.

Замена асновы лагарыфма

• Ад лагарыфма $\log_a b$ па аснове $a$ можна перайсці да лагарыфма па другой аснове $c$:

$\log_a b = \frac{\log_c b }{\log_c a}$

• Вынік: перастаноўка асновы і лагарыфмаванага выразу:

$\log_a b = \frac {1}{\log_b a}$

Лагарыфмічная функцыя

Лагарыфмічная функцыя адваротная да паказнікавай

Графікі лагарыфмічных функцый з асновамі: 2 (жоўты), e (чырвоны), 0.5 (сіні)

Двайковы лагарыфм і паказнікавая функцыя з асновай 2

Лагарыфм і паказнікавая функцыя з асновай 1/2

Асноўныя уласцівасці

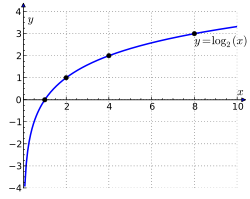
Калі разглядаць лагарыфмаваны лік як зменную, мы атрымаем лагарыфмічную функцыю $y=\log_a x$. Яна вызначана пры $a>0;\ a \ne 1; x>0$.

• Абсяг вызначэння: $x>0$.
• Абсяг значэнняў: $E(y)=(-\infty; + \infty )$.

Гэта крывая часта называецца лагарыфмікай.

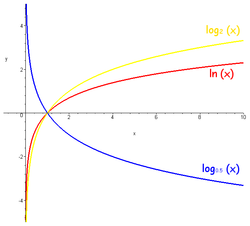
• З формулы замены асновы лагарыфма відаць, што графікі лагарыфмічных функцый з рознымі асновамі, большымі за адзінку, адрозніваюцца адзін ад аднаго толькі расцяжэннем уздоўж во́сі $y$:

$\log_b x = \frac{\log_a x}{\log_a b}$

• Графікі для асноў $a$ і $1/a$ сіметрычныя адносна во́сі x.

• З азначэння вынікае, што лагарыфмічная функцыя $y = \log_a x$ ёсць адваротнай да паказнікавай функцыі $y=a^x$, таму іх графікі сіметрычныя адносна бісектрысы першага і трэцяга квадрантаў (гл. рысунак). Як і паказнікавая, лагарыфмічная функцыя ёсць трансцэндэнтнай функцыяй.

• Лагарыфмічная функцыя ёсць строга нарастальнай пры $a > 1$ (гл. графікі) і строга спадальнай пры $0 < a < 1$. Графік любой лагарыфмічнай функцыі праходзіць праз кропку $(1;0)$. Функцыя непарыўная і бясконца дыферэнцавальная ўсюды на сваім абсягу вызначэння.

• Вось ардынат $(x=0)$ ёсць вертыкальнай асімптотай для лагарыфмічнай функцыі, бо:

$\lim_{x \to +0} \log_a x = - \infty$ пры $a > 1;$

$\lim_{x \to +0} \log_a x = + \infty$ пры $0 < a < 1$.

• Вытворная лагарыфмічнай функцыі:

$(\log_a x)' = \frac{1}{x \ln a}$

• Першаісная лагарыфмічнай функцыі:

$\int \log_a x\,dx = x \log_a x - \frac{x}{\ln a} + C$,

дзе $C$ — адвольная сталая.

• З пункту гледжання алгебры, лагарыфмічная функцыя ажыццяўляе (адзіны магчымы) ізамарфізм групы адносна множання дадатных рэчаісных лікаў і групы адносна складання ўсіх рэчаісных лікаў. Іншымі словамі, лагарыфмічная функцыя ёсць адзіным (вызначаным для ўсіх дадатных значэнняў аргумента) непарыўным развязкам функцыянальнага раўнання:

$f(xy)=f(x)+f(y)$

Натуральны лагарыфм

Прыведзеная вышэй агульная формула вытворнай выглядае найпрасцей у выпадку натуральнага лагарыфма:

$\frac{d}{dx} \ln x = \frac{1}{x}$

З гэтай прычыны ў матэматычных даследаваннях пераважна выкарыстоўваюць менавіта натуральныя лагарыфмы. Яны нярэдка з'яўляюцца пры развязанні дыферэнцыяльных раўнанняў, даследаванні статыстычных залежнасцей (напрыклад, размеркавання простых лікаў) і т. п.

Натуральны лагарыфм роўны плошчы пад гіпербалай

Праінтэграваўшы формулу для вытворнай у прамежку ад $x=1$ да $x=b$, мы атрымліваем:

$\ln b = \int\limits_1^b {\frac {dx}{x}}$

Інакш кажучы, натуральны лагарыфм роўны плошчы пад гіпербалай $y=\frac {1}{x}$ на азначаным прамежку x.

Нявызначаны інтэграл ад натуральнага лагарыфма лёгка знайсці інтэграваннем па частках:

$\int{\ln x\,\mathrm{d}x} = x\ln x-x+C$

У матэматычным аналізе і тэорыі дыферэнцыяльных раўнанняў вялікую ролю адыгрывае паняцце лагарыфмічнай вытворнай функцыі $f(x)$:

$\frac{d}{dx} \ln(f(x)) = \frac{f'(x)}{f(x)}$

Раскладанне ў шэраг і вылічэнне натуральнага лагарыфма

Раскладзём натуральны лагарыфм у шэраг Тэйлара блізу адзінкі:

$\ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \dots$

Гэты шэраг збягаецца пры $-1 < x \leqslant 1$. У прыватнасці:

$\ln 2 = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \dots$

Формула непрыдатная для практычнага вылічэння лагарыфмаў з-за таго, што шэраг збягаецца вельмі павольна і толькі на вузкім прамежку. Аднак нескладана атрымаць з яе зручнейшую формулу:

$\ln \left(\frac{1+x}{1-x}\right)=2\left(x+\frac{x^3}{3}+\frac{x^5}{5}+\frac{x^7}{7}+\dots\right)$

Гэты шэраг збягаецца хутчэй, і акрамя таго, цяпер левая частка формулы можа пада́ць лагарыфм любога дадатнага ліку.

Карыстацца апошняй формулай трэба так. Няхай $Z$ — лік, лагарыфм якога трэба вылічыць.

1) З раўнання

$Z = \frac{1+x}{1-x}$

знаходзім $x$:

$x = \frac{Z-1}{Z+1}$.

2) Вылічанае значэнне $x$ падстаўляем у шэраг і атрымліваем значэнне $\ln Z$.

Дадзены алгарытм ужо прыдатны да выкарыстання на практыцы пры вылічэнні значэнняў лагарыфмаў, аднак ён не найлепшы з пункту гледжання працаёмкасці. Існуюць больш дзейсныя алгарытмы.

Гранічныя стасункі

Прывядзем некалькі карысных граніц, якія ўтрымліваюць лагарыфмы.

$\lim_{x \to 0} \frac{\log_a (1+x)} {x} = \log_a e = \frac{1}{\ln a}$

$\lim_{x \to +0} x^b \log_a x = 0 \quad (b > 0)$

$\lim_{x \to +\infty} \frac{\log_a x}{x^b} = 0 \quad (b > 0)$

$\ln x = \lim_{n \to \infty} n \left(\sqrt[n]x -1 \right) = \lim_{n \to \infty} n \left(1-\frac{1}{\sqrt[n]{x}}\right)$

$\ln x = \lim_{h \to 0} \frac{x^h-1}h$

Іншыя ўласцівасці

• З тэарэмы Гельфо́нда вынікае, што калі $a, b$ — алгебраічныя лікі ($a \ne 1$), то $\log_a b$ або рацыянальны, або трансцэндэнтны. Пры гэтым лагарыфм рацыянальны і роўны $p \over q$ толькі ў тым выпадку, калі лікі $a, b$ стасуюцца як $a^p=b^q$.

• Сума $\sum_{k=1}^{n} \frac{1}{k}$ (частковая сума гарманічнага шэрагу) пры вялікіх $n$ паводзіць сябе як $\ln n + C$, дзе $C \approx 0{,}577215664\dots$ — сталая Ойлера - Маскероні.

Ужыванне на практыцы

Табліцы лагарыфмаў

Лагарыфмічныя табліцы

З уласцівасцей лагарыфма вынікае, што замест працаёмкага множання шматзначных лікаў дастаткова адшукаць (па табліцах) і скласці іхнія лагарыфмы, а потым па тых жа табліцах ("Антылагарыфмы") выканаць ступеняванне, г.зн. знайсці значэнне па ягоным лагарыфме. Выкананне дзялення адзрозніваецца толькі тым, што лагарыфмы адымаюцца.

Першыя табліцы лагарыфмаў выдаў Джон Нэпер (1614), і яны ўтрымівалі толькі лагарыфмы трыганаметрычных функцый, прычым з памылкамі. Незалежна ад яго свае табліцы надрукаваў Ёст Бюргі, друг Кеплера (1620). У 1617 годзе оксфардскі прафесар матэматыкі Генры Брыгс выдаў табліцы, якія ўжо ўлучалі дзесятковыя лагарыфмы лікаў ад 1 да 1000, з 8 (пазней — з 14) знакамі. Але і ў табліцах Брыгса выявіліся памылкі. Першае безпамылковае выданне на аснове табліц Георга Вегі (1783) з'явілася толькі ў 1857 годзе ў Берліне (табліцы Брэмікера, Carl Bremiker).

У Расіі першыя табліцы лагарыфмаў былі выдадзены ў 1703 годзе пры ўдзеле Л. Ф. Магніцкага. У СССР было выдадзена некалькі зборнікаў табліц лагарыфмаў:

1. Брадис В. М. Четырехзначные математические таблицы. М.: Дрофа, 2010, ISBN 978-5-358-07433-0. Табліцы Брадзіса, выдаваныя з 1921 года, выкарыстоўваліся ў навучальных установах і ў інжынерных разліках, якія не патрабавалі вялікай дакладнасці. Яны ўтрымлівалі мантысы дзесятковых лагарыфмаў і трыганаметрычных функцый, натуральныя лагарыфмы і некаторыя іншыя карысныя разліковыя прылады.
2. Вега Г. Таблицы семизначных логарифмов, 4-е издание, М.: Недра, 1971. Адмысловы зборнік для дакладных вылічэнняў.
3. Бремикер К. Логарифмо-тригонометрические таблицы. М.: Наука, 1962. 664 с. Класічныя шасцізначныя табліцы, зручныя для разлікаў з трыганаметрычнымі функцыямі.
4. Пятизначные таблицы натуральных значений тригонометрических величин, их логарифмов и логарифмов чисел, 6-е издание, М.: Наука, 1972.
5. Таблицы натуральных логарифмов, 2-е издание, в 2 томах, М.: Наука, 1971.
6. Десятизначные таблицы логарифмов комплексных чисел. М., 1952.

Лагарыфмічная лінейка

У 1620-я гады Эдмунд Ўінгейт і Ўільям Отрэд вынайшлі першую лагарыфмічную лінейку, якая да з'яўлення кішэнных калькулятараў была незаменнай вылічальнай прыладай інжынера. З дапамогай гэтай невялічкай прылады можна было хутка выконваць усе алгебраічныя аперацыі, у тым ліку з удзелам трыганаметрычных функцый. Дакладнасць разлікаў — каля 3 значных лічб.

Лагарыфмічная лінейка

Гл. таксама

• Камплексны лік
• Паказнікавая функцыя
• Камплексны лагарыфм
• Ступеняванне
• Лагарыфмічная лінейка
• Сістэмы злічэння
• Спіс інтэгралаў ад лагарыфмічных функцый

Вонкавыя спасылкі

• На ВікіСховішчы ёсць медыяфайлы па тэме Лагарыфм
• Colin Byfleet, Educational video on logarithms.
• Edward Wright, Translation of Napier’s work on logarithms.