Маса
| Маса | |
|---|---|
| Размернасць | M |
| Адзінкі вымярэння | |
| СІ | кг |
| СГС | г |

Ма́са (ад грэчаскага μᾶζα) — скалярная фізічная велічыня, якая колькасна характарызуе інертнасць цела, г. зн. яго здольнасць супраціўляцца знешнім уздзеянням. Чым большая маса цела, тым павольней яно будзе змяняць сваю хуткасць пад уплывам знешняй сілы, інакш кажучы — тым меншым будзе яго паскарэнне.
У механіцы паняцце масы было ўведзена І. Ньютанам. У класічнай механіцы маса з'яўляецца адытыўнай велічынёй, г. зн. маса складанай сістэмы ёсць сума мас яе частак.
Паняцце масы ўзнікае незалежна пры апісанні розных з'яў. Таму выдзяляюць наступныя віды масы:
- Інертная маса — мера інертнасці цела.
- Гравітацыйная маса — мера гравітацыйнага ўзаемадзеяння цел.
Сёння лічыцца, што гравітацыйная і інертная масы роўныя адна другой (гэта пацвярджаецца з высокаю дакладнасцю — парадку 10−13 — эксперыментальна[1], і ў большасці фізічных тэорый, у тым ліку ва ўсіх эксперыментальна пацверджаных, гэтыя масы разглядаюцца як дакладна роўныя), таму ў тым выпадку, калі гаворка ідзе не пра «новую фізіку», проста кажуць пра масу, не ўдакладняючы, якую з іх маюць на ўвазе.
У рэлятывісцкай механіцы масу вызначаюць як абсалютную велічыню 4-вектара энергіі-імпульсу[2]:
- дзе E — поўная энергія свабоднага цела, p — яго імпульс, c — хуткасць святла.
Пры такім азначэнні маса неадытыўная, але інварыянтная велічыня. Іншы раз (асабліва ў старой і папулярнай літаратуры) масу ў такім значэнні называюць інварыянтнай масай ці масай спакою.
Таксама ў папулярнай літаратуры сустракаецца паняцце рэлятывісцкая маса, якую вызначаюць як дзель поўнай энергіі цела на квадрат хуткасці святла.
Прырода масы — адна з найважнейшых нявырашаных праблем фізікі.
Інертная і гравітацыйная маса[правіць | правіць зыходнік]
Акрамя масы як меры інерцыі (інертнай масы) існуе паняцце гравітацыйнай масы як меры гравітацыйнага ўздзеяння цела на іншыя целы. Тэарэтычных падстаў лічыць, што гравітацыйная і інертная масы цела супадаюць, няма. Але шматлікія эксперыменты даказалі з высокай дакладнасцю, што інертная і гравітацыйная масы прапарцыянальныя адна адной, а гэта значыць, што пры звыклым выбары адзінак вымярэння значэнні абедзвюх мас супадаюць, і іх можна лічыць тоеснымі. Гэты факт названы А. Эйнштэйнам прынцыпам эквівалентнасці і пакладзены ў аснову агульнай тэорыі адноснасці.
Усе з'явы ў гравітацыйным полі адбываюцца дакладна гэтак жа, як у адпаведным полі сіл інерцыі, калі супадаюць напружанасці гэтых палёў і пачатковыя ўмовы для цел сістэмы.
Можна сказаць, што першая праверка прапарцыянальнасці двух відаў масы была выканана Галілеа Галілеем, які адкрыў усеагульнасць свабоднага падзення. Паводле вопытаў Галілея па назіранню свабоднага падзення цел, усе целы, незалежна ад іх масы і матэрыялу, падаюць з аднолькавым паскарэннем. Цяпер гэтыя вопыты можна растлумачыць так: павелічэнне сілы, дзеючай на больш масіўнае цела з боку гравітацыйнага поля Зямлі, цалкам ураўнаважваецца павелічэннем яго інертных уласцівасцей.
На роўнасць інертнай і гравітацыйнай мас звярнуў увагу яшчэ Ньютан, ён жа ўпершыню даказаў, што яны адрозніваюцца не больш чым на 0,1 % (інакш кажучы, роўныя з дакладнасцю да 10−3)[3]. На сёння гэтая роўнасць эксперыментальна праверана з вельмі вялікаю ступенню дакладнасці (адчувальнасць да адноснае рознасці інертнай і гравітацыйнай мас у найлепшым эксперыменце на 2009 год роўная (0,3±1,8)×10−13)[1].
Трэба адрозніваць «слабы прынцып эквівалентнасці» і «моцны прынцып эквівалентнасці». Моцны прынцып эквівалентнасці можна сфармуляваць так: у кожнай кропцы прасторы-часу ў адвольным гравітацыйным полі можна выбраць лакальна-інерцыяльную сістэму каардынат, такую, што ў дастаткова малым наваколлі вызначанай кропкі законы прыроды будуцб мець такую ж форму, як і ў не паскораных дэкартавых сістэмах каардынат, дзе пад «законамі прыроды» маюцца на ўвазе ўсе законы прыроды.
Слабы прынцып эквівалентнасці адрозніваецца тым, што словы «законы прыроды» замяняюцца ў ім словамі «законы руху свабодна падаючых часціц». Слабы прынцып — гэта не што іншае, як перафармулёўка назіраемай роўнасці гравітацыйнай і інертнай мас, тады як моцны прынцып з'яўляецца абагульненнем назіранняў за ўплывам гравітацыі на любыя фізічныя аб'екты.
Маса ў класічнай і рэлятывісцкай фізіцы[правіць | правіць зыходнік]
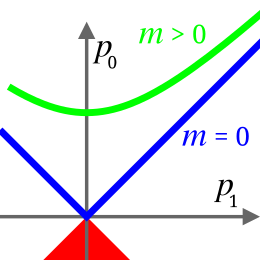
Вектары 4-імпульсу, праведзеныя ад пункта перасячэння восей да любога пункта на зялёнай гіпербале, маюць адну і тую ж (дадатную) даўжыню, г. зн. масу часціцы з такім чатырохімпульсам, і адрозніваюцца энергіяй і 4-хуткасцю часціцы.
Паскарэнне часціцы зводзіцца да руху канца 4-імпульсу па гіпербале.
Вектары 4-імпульсу, пабудаваныя ад пункта перасячэння восей да любога пункта на сініх паўпрамых, маюць нулявую даўжыню і могуць адносіцца толькі да часціц нулявой масы (напрыклад, фатонаў). Энергія такіх часціц (с дакладнасцю да множніка c) роўная модулю іх 3-імпульсу.
У нерэлятывісцкай класічнай механіцы маса ёсць велічыня адытыўная (маса сістэмы роўная суме мас цел-складнікаў сістэмы) і інварыянтная адносна змены сістэмы адліку.
У спецыяльнай тэорыі адноснасці маса неадытыўная, але таксама інварыянтная велічыня, вызначаная як абсалютная велічыня 4-вектара энергіі-імпульсу[2]:
дзе E — поўная энергія свабоднага цела, p — яго імпульс, c — хуткасць святла.
У выпадку адвольнай метрыкі прасторы-часу (як у агульнай тэорыі адноснасці) гэта азначэнне патрабуе некаторага абагульнення:
тут — метрычны тэнзар, — 4-імпульс.
Азначаная вышэй маса з'яўляецца рэлятывісцкім інварыянтам, г. зн. яна аднолькавая ва ўсіх сістэмах адліку. Калі перайсці ў сістэму адліку, дзе цела нерухомае, то — маса вызначаецца энергіяй спакою.
Асабліва проста выглядаюць гэтыя азначэнні ў сістэме адзінак, у якой хуткасць святла прынята за 1 (напрыклад, у планкаўскай ці ў прынятай у фізіцы элементарных часціц сістэме адзінак, у якой маса, імпульс і энергія вымяраюцца ў электронвольтах):
Варта, аднак, адзначыць, што часціцы з нулявою масаю (фатон і гіпатэтычны гравітон) рухаюцца ў вакууме з хуткасцю святла (c ≈ 300000 км/сек), і таму не існуе сістэмы адліку, дзе б яны не рухаліся. Наадварот, часціцы з ненулявою масаю заўсёды рухаюцца павольней чым святло ў вакууме.
Пра «масу спакою» і «рэлятывісцкую масу»[правіць | правіць зыходнік]
В сучаснай тэрміналогіі тэрмін маса прымяняецца замест тэрмінаў інварыянтная маса ці маса спакою і поўнасцю раўназначная ім па сэнсу. У некаторых выпадках (асабліва ў папулярнай літаратуры) гэта, аднак, удакладняецца яўна, каб пазбегнуць блытаніны з разуменнем тэрміна маса ў іншым — устарэлым — сэнсе, апісаным у гэтым падраздзеле.
У вялікай колькасці крыніц[4][5] пачатку і сярэдзіны XX стагоддзя, а таксама ў навукова-папулярных[6], уведзенае вышэй паняцце масы называлі «масай спакою», пры гэтым саму масу ўводзілі на аснове класічнага азначэння імпульсу
У такім выпадку і гаварылі, што маса цела расце з павелічэннем хуткасці. Пры такім азначэнні паняцце масы было раўназначным паняццю энергіі, а таксама патрабавала асобна ўводзіць «масу спакою», вымераную ва ўласнай СА, і «рэлятывісцкую масу» рушачага цела. Такі падыход быў распаўсюджаны на працягу доўгага часу[6], бо дазваляў праводзіць шматлікія аналогіі з класічнаю фізікаю, аднак у сучаснай навуковай літаратуры ўжываецца рэдка[7], бо ўносіць дадатковую блытаніну ў тэрміналогію, не даючы ніякіх новых вынікаў. Так званая рэлятывісцкая маса аказваецца адытыўнаю (у адрозненне ад масы спакою сістэмы, залежнай ад стану часціц-складнікаў). Бязмасавыя ж часціцы (напрыклад, фатоны) у такой тэрміналогіі аказваюцца са зменнаю масаю; акрамя таго, рэлятывісцкая маса ніколькі не спрашчаюць фармулёўку законаў дынамікі часціц.
Поўным адпаведнікам класічнага азначэння імпульсу праз масу і хуткасць у СТА трэба лічыць каварыянтную роўнасць:
дзе m — інварыянтная маса, а uμ — 4-хуткасць (вытворная ад 4-каарданаты па ўласнаму часу часціцы ; адзінкавы вектар, накіраваны ўздоўж сусветнай лініі часціцы).
Таксама можна запісаць каварыянтны адпаведнік другога закону Ньютана:
дзе — 4-паскарэнне (крывізна сусветнай лініі часціцы).
Маса складаных і няўстойлівых сістэм[правіць | правіць зыходнік]
Маса элементарнай часціцы пастаянная і аднолькавая ва ўсіх часціц данага тыпу і іх антычасціц. Аднак маса цел, складзеных з некалькіх элементарных часціц (напрыклад, ядра ці атама) можа залежаць ад іх унутранага стану. У прыватнасці, для ўстойлівых сістэм маса сістэмы заўсёды меншая за суму мас яе элементаў на велічыню, вядомую як дэфект масы, і роўную энергі сувязі, падзеленай на квадрат хуткасці святла.
Для сістэму, схільнай да распаду (напрыклад, радыеактыўнага), велічыня энергіі спакою вызначана толькі з дакладнасцю да пастаяннай Планка, падзеленай на час жыцця:
Пры апісанні такой сістэмы з дапамогаю квантавай механікі зручна разглядаць масу як камплексны лік з уяўнаю часткаю, роўнаю вышэйзгаданаму Δm.
Прырода масы[правіць | правіць зыходнік]
У тэарэтычнай фізіцы механізм узнікнення масы — тэорыя, якая спрабуе растлумачыць прыроду масы на аснове самых фундаментальных законаў фізікі. На сёння існуе некалькі мадэлей, якія прапануюць розныя погляды на прыроду масы. Задача ўскладняецца яшчэ і тым, што паняцце масы цесна звязана з гравітацыйным узаемадзеяннем, тэорыя якога дагэтуль не аб'яднана з папулярнай цяпер мадэллю фізікі часціц, вядомай як Стандартная мадэль.
Вызначэнне масы цела[правіць | правіць зыходнік]

Матэрыял — сплаў 90 % плаціны і 10 % ірыдыю.
Эталон захоўваецца ў штаб-кватэры Міжнароднага бюро мер і ваг у Сеўры.
Прынцып эквівалентнасці абгрунтоўвае вызначэнне масы цела распаўсюджаным спосабам узважвання. Масу нябесных цел разлічваюць на аснове характарыстык іх руху па арбітах. Адзінкай вымярэння масы ў сістэме СГС ёсць грам, а ў Міжнароднай сістэме СІ — кілаграм. Для вызначэння масы атамаў і малекул карыстаюцца атамнаю адзінкаю масы. Масу элементарных часціц вызначаюць або ў адзінках масы электрона me, або ў энергетычных адзінках, указваючы энергію спакою адпаведнай часціцы.
Адзінкі вымярэння масы[правіць | правіць зыходнік]


У Міжнароднай сістэме адзінак (СІ) маса вымяраецца ў кілаграмах. Адзінкай вымярэння масы ў сістэме СГС з'яўляецца грам (1⁄1000 кілаграма). Наогул кажучы, у любой сістэме вымярэння выбар асноўных (першасных) фізічных велічынь, іх адзінак вымярэння і іх колькасці адвольны — залежыць ад прыманага пагаднення і маса не заўсёды ўваходзіць у іх склад — так у сістэме МКГСС адзінка масы была вытворнай адзінкай і вымяралася у кгс/м•с² (пазначалася як «гэта значыць м.» або «інэртны»). У атамнай фізіцы прынята параўноўваць масу з атамнай адзінкай масы, у фізіцы цвёрдага цела — з масай электрона, у фізіцы элементарных часціц масу вымераюць у электронвольтах. Акрамя гэтых адзінак, якія выкарыстоўваюцца ў навуцы, існуе вялікая разнастайнасць гістарычных адзінак вымярэння масы, якія захавалі сваю асобную сферу выкарыстання: фунт, унцыя, карат, тона і інш. У астраноміі адзінкай для параўнання мас нябесных цел служыць маса Сонца.
Маса часам можа быць выяўлена ў тэрмінах даўжыні. Маса вельмі дробных часціц могуць быць вызначаны з дапамогай велічыні, зваротнай да комптанаўскай даўжыні хвалі: 1 см-1 ≈ 3.52×10-41кг. Маса вельмі вялікай зоркі або чорнай дзіркі можа быць атаясамленая з яе гравітацыйным радыусам: 1 см ≈ 6.73×1024кг.
Этымалогія і гісторыя паняцця[правіць | правіць зыходнік]
Слова маса (лац.: massa, ад стар.-грэч.: μαζα) першапачаткова ў антычныя часы азначала кавалак тэста. Пазней сэнс слова пашырыўся, і яно стала пазначаць цэльны, неапрацаваны кавалак адвольнага рэчыва; у гэтым сэнсе слова выкарыстоўваецца, напрыклад, у Авідзія і Плінія[8].
Маса як навуковы тэрмін была ўведзена Ньютанам як мера колькасці рэчыва, да гэтага прыродазнавец аперыраваў з паняццем вагі. У працы «Матэматычныя пачаткі натуральнай філасофіі» (1687) Ньютан спачатку вызначыў «колькасць матэрыі» ў фізічным целе як здабытак яго шчыльнасці на аб'ём. Далей ён указаў, што ў тым жа сэнсе будзе выкарыстоўваць тэрмін маса. Нарэшце, Ньютан ўводзіць масу ў законы фізікі: спачатку ў другі закон Ньютана (праз колькасць руху), а затым — у закон прыцягнення, адкуль адразу вынікае, што вага прапарцыянальная масе[9]. Ньютан відавочна паказаў на гэтую прапарцыянальнасць і нават праверыў яе на вопыце з усёй магчымай у тыя гады дакладнасцю: «Вызначаецца маса па вазе цела, бо яна прапарцыянальная вазе, што мной знойдзена вопытамі над маятнікамі, зрабленымі найдакладным чынам»[10]. (гэтыя вопыты Ньютан падрабязна апісаў у III томе сваіх «Пачаткаў»).
Фактычна Ньютан выкарыстоўвае толькі два разумення масы: як меры інерцыі і крыніцы прыцягнення[11]. Тлумачэнне яе як меры «колькасці матэрыі» — не больш чым наглядная ілюстрацыя, і яно падвергнулася крытыцы яшчэ ў XIX стагоддзі як нефізічнае і беззмястоўнае[12].
Доўгі час адным з галоўных законаў прыроды лічыўся закон захавання масы. Аднак у XX стагоддзі высветлілася, што гэты закон з'яўляецца абмежаваным варыянтам закона захавання энергіі, і ў многіх сітуацыях не выконваецца.
Паходжанне і гісторыя паняцця[правіць | правіць зыходнік]
Слова маса (лац.: massa, ад стар.-грэч.: μαζα) першапачаткова ў антычныя часы абазначала кусок цеста. Пазней сэнс слова пашырыўся, і яно стала абазначаць цэльны, неапрацаваны кавалак адвольнага рэчыва; у гэтым сэнсе слова ўжываецца, напрыклад, у Авідыя і Плінія[8].
Маса ў якасці навуковага тэрміна была ўведзена Ньютанам як мера колькасці рэчыва, да гэтага прыродазнаўцы карысталіся паняццем вагі. У працы «Матэматычныя пачаткі натуральнай філасофіі» (1687) Ньютан спачатку вызначыў «колькасць матэрыі» ў фізічным целе як здабытак яго шчыльнасці на аб'ём. Далей ён патлумачыў, што ў тым жа сэнсе будзе ўжываць тэрмін маса. Нарэшце, Ньютан уводзіць масу ў законы фізікі: спачатку ў другі закон Ньютана (праз колькасць руху), а затым — у закон прыцягнення, адкуль адразу вынікае, што вага прапарцыянальная масе[9]. Ньютан яўна звярнуў увагу на гэту прапарцыянальнасць і нават праверыў яе на вопыце з усёю магчымаю ў тыя гады дакладнасцю: «Вызначаецца маса па вазе цела, бо яна прапарцыянальная вазе, што мною выяўлена вопытамі над маятнікамі, праведзенымі найдакладнейшым чынам»[10] (гэтыя вопыты Ньютан падрабязна апісаў у III томе сваіх «Пачаткаў»).
Фактычна Ньютан ужывае паняцце масы толькі ў двух сэнсах: як меры інерцыі і крыніцы прыцягнення[13]. Тлумачэнне яе як меры «колькасці матэрыі» — не больш чым наглядная ілюстрацыя, і яно крытыкавалася яшчэ ў XIX стагоддзі як нефізічнае і беззмястоўнае[14].
Доўгі час адным з галоўных законаў прыроды лічыўся закон захавання масы. Але ў XX стагоддзі высветлілася, што гэты закон з'яўляецца абмежаваным варыянтам закону захавання энергіі, і ў многіх выпадках не выконваецца.
Гл. таксама[правіць | правіць зыходнік]
Зноскі[правіць | правіць зыходнік]
- ↑ а б S. Schlamminger, K.-Y. Choi, T.A. Wagner, J.H. Gundlach, and E.G. Adelberger. Test of the Equivalence Principle Using a Rotating Torsion Balance // Phys. Rev. Lett.. — 2008. — В. 4. — Т. 100. — DOI:10.1103/PhysRevLett.100.041101 — arΧiv:0712.0607
- ↑ а б Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7., § 9. Энергия и импульс.
- ↑ Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5.
- ↑ Фок В. А. Теория пространства, времени и тяготения. — М.: Государственное издательство технико-теоретической литературы, 1955. — 504 с.
- ↑ Мёллер К. Теория относительности = The theory of relativity. Clarendon Press. Oxford. 1972.. — М.: Атомиздат, 1975. — 400 с.
- ↑ а б Л. Б. Окунь, Успехи физических наук, 2000, т. 170, с. 1366
- ↑ Окунь Л. Б. Понятие массы (Масса, энергия, относительность) (Методические заметки) // УФН. — 1989. — Т. 158. — С. 511—530.
- ↑ а б Джеммер, М. 1967, Глава I.
- ↑ а б Спасский Б. И.. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
- ↑ а б И. Ньютон. Математические начала натуральной философии, том I, определение 1.
- ↑ Тюлина И. А. Об основах ньютоновой механики (к трехсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: МГУ, 1989. — В. 36. — С. 184-196..
- ↑ Мах Э. Механика. Историко-критический очерк её развития. Ижевск: НИЦ РХД, 2000, 456 с., ISBN 5-89806-023-5.
- ↑ Тюлина И. А. Об основах ньютоновой механики (к трехсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: МГУ, 1989. — В. 36. — С. 184-196.
- ↑ Мах Э. Механика. Историко-критический очерк её развития. Ижевск: НИЦ РХД, 2000, 456 с., ISBN 5-89806-023-5.
Літаратура[правіць | правіць зыходнік]
- Джеммер, Макс. Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
- Переиздание: Едиториал УРСС, 2003, ISBN 5-354-00363-6.
- Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 (1989)
- Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
- L. B. Okun On the concepts of vacuum and mass and the search for higgs(англ.) // Modern Physics Letters A. — 2012. — Vol. 27. — P. 1230041. — DOI:10.1142/S0217732312300418 — arΧiv:1212.1031
- Спасский Б. И.. История физики. М., «Высшая школа», 1977. Том 1, часть 1-я.
- Gordon Kane. The Mysteries of Mass Архівавана 28 ліпеня 2011.. // Scientific American. June 27, 2005.















