Аптычны пінцэт

Апты́чны пінцэ́т (англ.: Optical tweezers), часам ла́зерны пінцэ́т або апты́чная па́стка — аптычны інструмент, які дазваляе маніпуляваць мікраскапічнымі аб'ектамі з дапамогай лазернага святла (якое звычайна атрымліваецца ад лазернага дыёда). Ён дазваляе прыкладаць к дыэлектрычным аб'ектам сілы ад фемтаньютанаў да нананьютанаў і вымяраць адлегласці ад некалькіх нанаметраў да мікронаў. У апошнія гады аптычныя пінцэты пачалі выкарыстоўваць у біяфізіцы для вывучэння структуры і прынцыпу работы бялкоў.
Гісторыя[правіць | правіць зыходнік]
Яшчэ ў XVII стагоддзі нямецкі астраном Іаган Кеплер, зыходзячы з назіранняў за хвастамі камет пры набліжэнні да Сонца, выказаў здагадку, што святло можа аказваць ціск на рэчыва. Хоць пазней аказалася, што гэта не адзіны механізм гэтага адхілення, ідэя Кеплера аказалася плённай для развіцця астраноміі. Напрыклад, было паказана, што светлавы (радыяцыйны ціск) — адзін з самых галоўных механізмаў, адказных за дынаміку часціц у міжзорнай прасторы.
Праз два стагоддзі пасля даследаванняў Кеплера Джэймс Максвел разлічыў значэнне светлавога ціску з дапамогай сваёй тэорыі электрамагнітных з'яў. Гэты эфект быў эксперыментальна вымераны ў 1910 годзе расійскім фізікам Пятром Лебедзевым, які паказаў, што святло аказвае ціск на целы. У 1970 годзе, дзеянне сіл, звязаных з рассейваннем і градыентамі інтэнсіўнасці святла, на часціцы мікронных памераў было апублікавана ў навуковай літаратуры Артурам Ашкінам (англ.: Arthur Ashkin), супрацоўнікам Bell Labs[1].
Шмат пазней, Ашкін і калегі паведамілі аб першым назіранні таго, што цяпер называецца аптычнай пасткай, г. зн. сфакусіраванага пучка святла, здольнага ўтрымліваць мікраскапічныя часціцы (10 нм - 10 мкм) нерухома ў трох вымярэннях[2].
Падобны прынцып выкарыстоўваецца і для лазернага ахалоджвання — метаду, які дазволіў давесці тэмпературу атамаў у аптычнай пастцы да найменшых значэнняў, недасягальных іншымі сродкамі. Метад быў прапанаваны савецкім фізікам Лятохавым ў 1968 годзе [3] і рэалізаваны той жа групай Ашкіна ў 1978 годзе[4]. Даследчую працу працягнуў Стывен Чу (англ.: Steven Chu) (у мінулым супрацоўнік Ашкіна), які за гэту працу атрымаў Нобелеўскую прэмію ў 1997 годзе.
У 1980-х гадах Стывен Блок (англ.: Steven Block) і Говард Берг (англ.: Howard Berg) упершыню ўжылі тэхналогію аптычнага пінцэта ў біялогіі, выкарыстоўваючы яе, каб утрымаць бактэрыю з мэтай вывучэння бактэрыяльных жгуцікаў. Ужо ў 1990-х гадах даследчыкі, такія як Карлас Бустаманте (англ.: Carlos Bustamante), Джэймс Спудыч (англ.: James Spudich) і Стывен Блок, ужылі прынцып аптычнай сілавой спектраскапіі, каб характарызаваць біялагічныя рухавікі малекулярнага маштабу. Гэтыя малекулярныя маторы сустракаюцца паўсюдна ў біялогіі, і адказваюць за перамяшчэнне клетак, змену іх формы і за транспарт у межах клеткі. Аптычныя пасткі дазволілі біяфізікам назіраць сілы і дынаміку малекулярных матораў на прыкладзе адной малекулы. Аптычная сілавая спектраскапія дазволіла лепш зразумець стахастычную (выпадковую) прыроду малекул, якія выпрацоўваюць энергію.
Аптычны пінцэт аказаўся карысным таксама і ў іншых галінах біялогіі. Напрыклад, у 2003 годзе метад аптычнага ўтрымання быў выкарыстаны для сартавання клетак. Ствараючы вялікую аптычную інтэнсіўнасць над узорам, клеткі можна сартаваць па іх уласных аптычных характарыстыках[5][6]. Аптычны пінцэт таксама выкарыстоўваецца для даследавання цыташкілетаў, вымярэння вязкасці і пругкасці біяпалімераў і вывучэння руху клетак.
Фізічныя прынцыпы[правіць | правіць зыходнік]
Аб'екты, калі ўявіць іх у выглядзе маленькіх дыэлектрычных сфер, ўзаемадзейнічаюць з электрычным полем, створаным светлавой хваляй, за кошт індуцыраванага на сферы дыпольнага моманту. У выніку ўзаемадзеяння гэтага дыполя з электрычным полем электрамагнітнай хвалі, аб'ект перамяшчаецца ўздоўж градыента электрычнага поля. Акрамя градыентнай сілы, на аб'ект таксама дзейнічае сіла, выкліканая ціскам (адбіццём) святла ад яго паверхні. Гэта сіла штурхае сферу па кірунку пучка святла. Аднак, калі прамень святла моцна сфакусіраваны, велічыня градыента інтэнсіўнасці можа пераўзыходзіць велічыню ціску святла[7].
Больш падрабязны аналіз заснаваны на двух механізмах, прапанаваных Ашкінам, у залежнасці ад памеру часціцы. У тэорыі рассейвання святла вядома, што механізм рассейвання святла часціцай залежыць ад суадносін памераў часціцы і даўжыні светлавой хвалі. Калі памер рассейваючых часціц значна меншы за даўжыню хвалі святла, то мае месца рэлееўскае рассейванне. Калі святло рассейваецца на часціцах (пыл, дым, водныя кропелькі), якія маюць памер большы за даўжыню хвалі, гэта рассейванне Мі (па імені нямецкага фізіка Густава Мі). Рассейванне Мі адказвае за белы і шэры колер аблокаў.
Прытрымліваючыся той жа ідэі, Ашкін прапанаваў выкарыстоўваць для матэматычнага аналізу аптычнага мікраманіпуліравання два розныя метады, а іменна:
- падыход хвалевай оптыкі для міеўскіх часціц (калі дыяметр часціцы большы за даўжыню хвалі святла d > λ)
- і прыбліжэнне электрычнага дыполя для рэлееўскіх часціц (d < λ).
Хвалевая оптыка[правіць | правіць зыходнік]
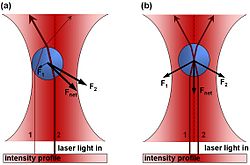
Пры аналізе з выкарыстаннем хвалевай оптыкі, дастаткова разгледзець працэсы праламлення і адбіцця святла ад мікрасферы дастаткова, каб прааналізаваць уцягванне ў аптычную пастку (гл. малюнак справа).
Самы просты разлік дзеючых сіл у межах падыходу хвалевай оптыкі грунтуецца на геаметрычнай оптыцы. Пры адлюстраванні і праламленні імпульс святла мяняецца. У сваю чаргу, гэта змяненне імпульсу (фатона як часціцы), згодна з другім законам Ньютана, прыводзіць да ўзнікнення сілы.
З дапамогай простай дыяграмы прамянёў і вектара сілы можна паказаць, што на мікрасферы дзейнічаюць дзве розныя аптычныя сілы, абумоўленыя інерцыяй падаючага і пераломленага святла. Як відаць з дыяграмы, выніковая сіла штурхае сферу ў напрамку да вобласці найвышэйшай інтэнсіўнасці прамяня. Такая сіла называецца градыентнай сілай.
Ашкін у сваім першым эксперыменце[1] выкарыстаў міліватны гаусаўскі пучок аднамодавага (TEM00) аргонавага лазера з даўжынёй хвалі 514,5 нм сфакусіраванага ў пляму дыяметрам w0=6,2 мікрона. Ён рухаў з дапамогай гэтага пучка латэксныя сферы дыяметрам 0,51; 1,31 і 2,68 мікрона ў вадзе і паветры. Для сфер радыуса r=1,31 мікрона, змешчаных у ваду, і магутнасці лазера P=19 мВт хуткасць сфер дасягала 26 мкм/с. А з ацэнкі па формуле
дзе
- q — доля святла эфектыўна адлюстраванага ад сферы (0,062),
- c — хуткасць святла,
- η — дынамічная вязкасць вадкасці (1 МПа·с для вады),
атрымалася значэнне 29 μм/с. А адпаведная сіла, дзеючая на часціцу атрымліваецца з закона Стокса
і складае 730 фН.
У паветры максімальная хуткасць для кропель вады дыяметрам 5 мікрон пры магутнасці лазера 50 мВт склала 0,25 см/c[1].
Каб даследуемы аб'ект быў нерухомы, неабходна ўраўнаважыць сілу, выкліканую ціскам святла. Гэта можна зрабіць за кошт двух сустрэчных пучкоў святла, якія штурхаюць сферу ў процілеглых кірунках, або з дапамогай моцна сфакусаванага гаусавага пучка (з высокай лікавай апертурай, NA>1,0), каб ураўнаважыць ціск святла высокай градыентнай сілай.
З іншага боку, у рэлееўскім рэжыме, часціцы не абмежаваныя па форме. Наогул, для меншых часціц патрэбна меншая сіла прыцягвання. У большасці выпадкаў, для тлумачэння механізму работы лазернага пінцэта для любой формы часціц выкарыстоўваюць мадэль прыведзенага дыполя. Электрамагнітнае выпраменьванне будзе індуцыраваць дыпольны момант, або палярызацыю, у дыэлектычнай часціцы. Сіла ўзаемадзеяння гэтага дыполя са святлом прыводзіць да градыентнай сілы прыцягвання.
Падрабязная інфармацыя пра прыбор аптычнай пасткі прыведзена на сайце лабараторыі Стывена Блока[8].
Прыбліжэнне электрычнага дыполя[правіць | правіць зыходнік]
У выпадках, калі дыяметр злоўленай у пастку часціцы значна меншы, чым даўжыня хвалі святла, умовы адпавядаюць выпадку рассейвання Рэлея, і часціцу можна разглядаць як кропкавы дыполь у неаднародным электрамагнітным полі. Сіла, якая дзейнічае на зараджаную часціцу ў электрамагнітнай вобласці, вядома як сіла Лорэнца:
Сіла, дзеючая на дыполь, раўняецца суме сіл, дзеючых на асобныя зарады
Адлегласць паміж зарадамі ў дыполі малая, таму вонкавае электрычнае поле можна раскласці ў наваколлі першага зарада ў рад Тэйлара, адкінуўшы пры гэтым нелінейныя члены:
Заўважце, што скарачаецца. Раскрываем дужкі і замяняем здабытак зарада на адлегласць дыпольным момантам часціцы атрымаем
дзе другая роўнасць атрымана на аснове дапушчэння, што дыпольны момант часціцы прама прапарцыянальны вонкаваму электрычнаму полю (гэта значыць ).
Улічваючы тоеснасць для аператара з вектарнага аналізу:
і адно з ураўненняў Максвела:
атрымаем
Другі складнік у апошняй роўнасці — вытворная па часе велічыні, якая звязаная праз пастаянны множнік з вектарам Пойнтынга, які апісвае магутнасць выпраменьвання, якое праходзіць праз адзінкавую пляцоўку. Калі лічыць, што магутнасць лазера не залежыць ад часу, то вытворная гэтага складніка будзе роўная нулю, і сіла запішацца ў выглядзе[9]
Квадрат велічыні электрычнага поля роўны інтэнсіўнасці прамяня як функцыя каардынат. Таму, вынік паказвае, што сіла, якая дзейнічае на дыэлектрычную часціцу, пры набліжэнні кропкавага дыполя, прапарцыянальная градыенту інтэнсіўнасці пучка. Іншымі словамі, апісаная тут сіла (градыентная сіла) прыводзіць да прыцягнення часціцы ў вобласць з самай высокай інтэнсіўнасцю.
Cіла, якая ўзнікае пры рассейванні святла, залежыць лінейна ад інтэнсіўнасці прамяня, папярочнага сячэння часціцы і паказчыка праламлення асяроддзя, у яком знаходзіцца пастка (напрыклад, вада), працуе супраць градыентнай сілы ў восевым кірунку пасткі, прыводзячы да таго, што раўнаважнае становішча ссоўваецца трохі ўніз ад становішча максімуму інтэнсіўнасці.
Лазерны пінцэт, заснаваны на альтэрнатыўных рэжымах працы лазера[правіць | правіць зыходнік]
З часу вынаходства першага лазернага пінцэта, заснаванага на адным гаусавым пучку (фундаментальная лазерная мода TEM00) А. Ашкінам у 1986[10], канцэпцыя аднамодавых лазерных пучкоў развілася за кошт выкарыстання лазерных мод высокага парадку, гэта значыць эрміт-гаусавых пучкоў (TEMnm), лагер-гаусавых пучкоў (LG, TEMpl) і бесэлевых пучкоў (Jn).
Лагер-гаусавыя пучкі валодаюць унікальнай уласцівасцю: ўцягваць у аптычную пастку аптычна адбіваючыя і паглынаючыя часціцы. Пучкі з кругавой палярызацыяй маюць спінавы арбітальны момант і могуць круціць часціцы. У лагер-гаусавых пучкоў таксама ёсць уласны вуглавы момант, які можа круціць часціцы вакол цэнтра пучка[11][12]. Гэты эфект назіраецца без знешняй механічнай ці электрычнай рэгуляцыі прамяня. Акрамя лагер-гаусавых пучкоў, бесэлевыя пучкі як нулявога, так і вышэйшых парадкаў маюць арбітальны момант, а таксама ўнікальную ўласцівасць адначасова ўтрымліваць шмат часціц на некаторай адлегласці[13].
Мультыплексныя лазерныя пінцэты[правіць | правіць зыходнік]
Тыповая ўстаноўка мае толькі адзін ці два лазерныя прамяні. Больш складаныя эксперыменты патрабуюць, каб адначасова працавала шмат пастак. Гэтага можна дасягнуць, выкарыстоўваючы адзін лазер, святло якога праходзіць праз акуста-аптычны мадулятар або праз люстэркі, якія кіруюцца электронікай. З дапамогай гэтых прылад лазернае выпраменьванне можна падзяліць у часе на некалькі прамянёў, а з дапамогай дыфракцыйных аптычных элементаў — разбіць на некалькі прамянёў у прасторы[14][15][16][17].
Лазерныя пінцэты, заснаваныя на аптычных валокнах[правіць | правіць зыходнік]
У гэтым тыпе прыбораў лазернае выпраменьванне падаецца праз аптычнае валакно. Калі адзін канец аптычнага валакна ўтварае паверхню, падобную па ўласцівасцях на лінзу, гэта дазваляе сфакусіраваць святло ў аптычнай пастцы з вялікай лікавай апертурай[18].
Калі ж канцы валакна не выпуклыя, лазернае святло будзе адхіляцца, і таму ўстойлівую аптычную пастку можна стварыць толькі з дапамогай двух канцоў валокнаў па абодва бакі ад аптычнай пасткі, і балансуючых градыентных сіл і ціскаў святла. Градыентныя сілы ўтрымліваюць часціцы ў папярочным кірунку, тады як восевая аптычная сіла ўзнікае ад ціску двух сустрэчных пучкоў святла, якія выходзяць і распаўсюджваюцца з двух аптычных валокнаў. Раўнаважная z-пазіцыя сферы ў такой пастцы — пазіцыя, дзе ціскі святла раўняюцца адзін аднаму. Такія лазерныя пінцэты былі ўпершыню створаны А. Канстэблям[19] і Дж. Гюкам[20], якія выкарыстоўвалі гэту методыку для расцяжэння мікрачасціц. Маніпулюючы ўваходнай магутнасцю з абодвух канцоў оптавалакна, можна рэгуляваць расцягваючую сілу. Такую сістэму можна выкарыстоўваць, каб вымяраць вязкасць і эластычнасць клетак, з адчувальнасцю, дастатковай, каб адрозніць розныя цыташкілеты, напрыклад, эрытрацытаў чалавека і фібрабластаў мышэй. Нядаўнія даследаванні дасягнулі вялікага поспеху ў адрозніванні ракавых клетак ад нармальных[21].
Аптычныя пінцэты ў сартаванні клетак[правіць | правіць зыходнік]

Адна з найбольш распаўсюджаных сістэм сартавання клетак выкарыстоўвае метад флуарэсцэнтнай праточнай цытаметрыі. У гэтым метадзе суспензія біялагічных клетак сартуецца ў некалькі кантэйнераў згодна з флюарэсцэнтнымі характарыстыкамі кожнай клеткі ў патоку. Працэс сартавання кантралюецца электрастатычнай сістэмай адхілення, якая накіроўвае клетку да вызначанага кантэйнера змяненнем напружання прыкладзенага электрычнага поля.
У аптычна кіруемай сістэме сартавання клеткі прапускаюць праз двух- або трохмерныя аптычныя рашоткі. Без індуцыруемага электрычнага напружання, клеткі сартуюцца па іх уласцівасцях праламлення святла. Група даследчыкаў пад кіраўніцтвам Кішана Далакіа распрацавала методыку выкарыстання дыфракцыйнай оптыкі і іншых аптычных элементаў для стварэння такіх аптычных рашотак[22]. З іншага боку, група вучоных з універсітэта горада Таронта пабудавала аўтаматычную сартавальную сістэму, выкарыстоўваючы прасторавы мадулятар святла[23].
Галоўны механізм сартавання — размяшчэнне вузлоў аптычнай рашоткі. Калі паток клетак праходзіць праз аптычныя рашоткі, сілы трэння часціц непасрэдна канкурыруюць з аптычнай градыентнай сілай ад суседняга вузла аптычнай рашоткі. Змяняючы размяшчэнне вузлоў, можна стварыць аптычную дарожку, па якой будуць рухацца клеткі. Але такая дарожка будзе эфектыўнай толькі для клетак з пэўным каэфіцыентам праламлення, якія і будуць эфектыўна адхіляцца. Рэгулюючы хуткасць патоку клетак і магутнасць святла, можна атрымаць добрае аптычнае сартаванне клетак.
Спаборніцтва сіл у сістэме сартавання мае патрэбу ў дакладнай юсціроўцы, каб дасягнуць высокай эфектыўнасці аптычнага сартавання. На сённяшні дзень у Сент-Эндрускам універсітэце створана вялікая даследчая група для працы над гэтай праблемай. У выпадку поспеху гэта тэхналогія зможа замяніць традыцыйнае флюарэсцэнтнае сартаванне клетак[24].
Лазерныя пінцэты, заснаваныя на затухаючых палях[правіць | правіць зыходнік]
Затухаючае поле — электрамагнітнае поле, якое пранікае ўглыб рэчыва, напрыклад пры поўным унутраным адлюстраванні[25][26]. Электрычнае поле ў светлавой хвалі затухае па экспаненце. Затухаючае поле знайшло цэлы шэраг прымяненняў у аптычнай мікраскапіі нанаметровых аб'ектаў, аптычная мікраманіпуляцыя (лазерныя пінцэты) становіцца яшчэ адным яго дастасаваннем.
У лазерных пінцэтах непарыўнае затухаючае поле можа быць створана, калі святло распаўсюджваецца праз аптычны хвалявод (шматразовае поўнае ўнутранае адлюстраванне). Выніковае затухаючае поле мае накіраваны імпульс, і будзе рухаць мікрачасціцы ўздоўж напрамку свайго распаўсюджання. Гэты эфект быў адкрыты вучонымі С. Каватай і Т. Сугіурай у 1992 годзе[27][28]. Яны паказалі, што поле можа звязваць часціцы, якія знаходзяцца на адлегласці каля 100 нанаметраў. Гэта прамое звязванне поля разглядаецца як тунэляванне фатонаў праз прамежак паміж прызмай і мікрачасціцамі. У выніку ўзнікае накіраваная аптычная сіла.
Нядаўняя версія лазерных пінцэтаў, заснаваных на затухаючым полі, выкарыстоўвае вялікую паверхню з аптычнай рашоткай, што дазваляе адначасова звязваць шмат часціц і накіроўваць іх у патрэбным кірунку без выкарыстання хвалявода. Такая методыка называецца «бязлінзавай аптычнай пасткай» (англ.: lensless optical trapping, LOT)[29]. Дакладна накіраванаму руху часціц садзейнічае рашотка Рончы (англ.: Ronchi Ruling), або стварэнне выразных аптычных патэнцыяльных ям у шкляной пласцінцы. Цяпер навукоўцы таксама працуюць над факусіроўкай затухаючых палёў.
Непрамы падыход да аптычных пінцэтаў[правіць | правіць зыходнік]
Мін Ву, прафесар факультэта радыётэхнікі і інфарматыкі ў Каліфарнійскім універсітэце стварыў новы оптаэлектронны пінцэт. Ву ператварыў аптычную энергію ад маламагутных святловыпрамяняльных дыёдаў у электрычную энергію праз фотаправодную паверхню. Ідэя — дазволіць дыёду ўключаць фотаправодны матэрыял у яго праекцыі. Гэты метад мае высокую гнуткасць уключэння розных аптычных ландшафтаў, бо аптычны шаблон лёгка паддаецца ператварэнню праз аптычнае праектаванне.
Працэс маніпуляцыі ажыццяўляецца з дапамогай змянення электрычнага поля, якое ўключаецца светлавым шаблонам. Часціцы будуць ці прыцягвацца, ці адштурхоўвацца ад узбуджанага вузла ў залежнасці ад свайго электрычнага зараду. Часціцы, якія завіслі ў вадкасці, будуць успрымальныя да электрычнага зараду дзякуючы іонам у вадкасці, працэс, вядомы як дыэлектрафарэз.
Адно з прымяненняў гэтага метаду — сартаванне жывых і мёртвых клетак. Сартаванне грунтуецца на тым, што жывыя клеткі напоўнены электралітам, а мёртвыя — не, і іх можна лёгка раздзяліць. Такая сістэма дазваляе маніпуляваць 10000 клеткамі або часціцамі адначасова[30].
Аптычнае звязванне[правіць | правіць зыходнік]
Калі мноства мікрачасціц падтрымліваецца монахраматычным лазерным пучком, размяшчэнне мікрачасціц у межах аптычнай пасткі залежыць ад пераразмеркавання аптычных сіл паміж часціцамі. Можна сказаць, што кластар мікрачасціц звязваецца разам святлом. Першыя эксперыменты па аптычнаму звязванню былі пастаўлены ў лабараторыі Яўгена Галоўчанкі ў Гарвардскім універсітэце [31].
Вымярэнне аптычных сіл[правіць | правіць зыходнік]
У цяперашні час сіла прыцягвання можа быць вымерана як на адна-, так і на двухпучковых лазерных пінцэтах (фатонны сілавы мікраскоп)[32][33]. Нядаўна пачаліся работы па вымярэнню аптычных сіл у галаграфічных лазерных пінцэтах, каб дасягнуць высокай дакладнасці пазіцыянавання пастак для асобных атамаў[34][35] [36]. Асноўны прынцып вымярэння аптычнай сілы лазерных пінцэтаў — перадача імпульсу святла, звязаная з праламленнем святла на часціцах. Змена кірунку распаўсюджвання святла як у папярочным, так і ў падоўжным кірунку забяспечвае сілу, якая дзейнічае на аб'ект. Таму найменшая папярочная сіла можа быць вымерана па адхіленню пучка, які прайшоў скрозь часціцу. Такое адхіленне можна лёгка вымераць з дапамогай дэтэктара восевай пазіцыі. Самы просты з якіх — квадрантны фотадыёд: пласцінка, падзеленая на чатыры сектары, з пучком святла, сфакусіраваным у яе цэнтры. Пры часціцы ў цэнтры на сектары падае святло роўнай магутнасці, але калі на часціцу дзейнічае сіла, магутнасці ўжо не будуць роўныя, і іх розніца прапарцыйная гэтай сіле.
Такі прынцып можа прымяняцца з любымі лазернымі пінцэтамі. Найбольшай праблемай пры такіх вымярэннях будзе броўнаўскі рух (шум). Тым не менш, сілы парадку піканьютана і зрух парадку нанаметраў звычайна можна вымераць[37].
Заўвагі[правіць | правіць зыходнік]
- ↑ а б в Ashkin A., «Acceleration and Trapping of Particles by Radiation Pressure», Phys. Rev. Lett. 24, 156 (1970). DOI:10.1103/PhysRevLett.24.156
- ↑ Ashkin A., Dziedzic J. M. & Yamane T., «Optical trapping and manipulation of single cells using infrared laser beams», Nature 330, 769 (1987). DOI:10.1038/330769a0
- ↑ Letokhov V. S., et. al. Cooling and trapping of atoms and molecules by a resonant laser field. Opt. Commun. 19, 72 (1976) DOI:10.1016/0030-4018(76)90388-6
- ↑ Ashkin A. Trapping of Atoms by Resonance Radiation Pressure Phys. Rev. Lett. 40, 729 (1978) DOI:10.1103/PhysRevLett.40.729
- ↑ Macdonald M. P., Spalding G. C. & Dholakia K., «Microfluidic sorting in an optical lattice», Nature 426, 421 (2003). DOI:10.1038/nature02144
- ↑ Optical Peristalsis by Brian A. Koss and David G. Grier The University of Chicago
- ↑ Advanced techniques for optical manipulation
- ↑ Construction of optical tweezers Архівавана 20 сакавіка 2006. by Steven M. Block, Princeton University
- ↑ Gordon J. P. Radiation forces and Momenta in Dielectric Media Phys. Rev. A 8, 14 (1973) DOI:10.1103/PhysRevA.8.14
- ↑ Ashkin A. «Optical trapping and manipulation of neutral particles using lasers», PNAS 94, 4853 (1997). [1] Архівавана 24 верасня 2015.
- ↑ Structure of Optical Vortices by J. E. Curtis and D. G. Grier, The University of Chicago
- ↑ Optical Spanners Архівавана 22 сакавіка 2004. by M. Padgett, University of Glasgow
- ↑ Bessel Beams
- ↑ Soft matter Lab by Prof. E. Dufresne, Yele University
- ↑ D. Grier’s Home Page
- ↑ Programmable Phase Optics Group Архівавана 25 мая 2006. Risø National Laboratory,
- ↑ Optical tweezers Архівавана 14 мая 2013. Glasgow University
- ↑ Hu Z, Wang J, Liang J, «Manipulation and arrangement of biological and dielectric particles by a lensed fiber probe», Optics Express, 12, 4123 (2004). [2]
- ↑ A. Constable et al., «Demonstration of a fiber-optical light-force trap»Opt. Lett. 18, 1867 (1993). [3]
- ↑ Guck J. et al., «Optical Deformability of Soft Biological Dielectrics» Phys. Rev. Lett. 84, 5451 (2000). DOI:10.1103/PhysRevLett.84.5451
- ↑ Jochen Guck, Stefan Schinkinger, Bryan Lincoln, Falk Wottawah, Susanne Ebert, Maren Romeyke, Dominik Lenz, Harold M. Erickson, Revathi Ananthakrishnan, Daniel Mitchell, Josef Käs, Sydney Ulvick and Curt Bilby, «Optical Deformability as an Inherent Cell Marker for Testing Malignant Transformation and Metastatic Competence» Архівавана 9 лістапада 2007., Biophys. J., 88:3689-3698 (2005)
- ↑ Macdonald M. P., Spalding G. C. & Dholakia K., «Microfluidic sorting in an optical lattice», Nature 421, 421 (2003). DOI:10.1038/nature02144
- ↑ Grover S. C. «Automated single-cell sorting system based on optical trapping» J Biomed Opt. 6, 14 (2001). [4]
- ↑ IRC Scotland
- ↑ Evanescent Field Polarization and Intensity Profiles Архівавана 21 ліпеня 2006. by D. Axelrod et al.
- ↑ What Everyone Needs to Know About Evanescent Fields Архівавана 5 верасня 2006. by T. Hunt Harvard University.
- ↑ Kawata S. and Sugiura T. «Movement of micrometer-sized particles in the evanescent field of a laser beam» Opt. Lett. 17, 772 (1992).
- ↑ Okamoto K. & Kawata S., «Radiation Force Exerted on Subwavelength Particles near a Nanoaperture» Phys. Rev. Lett. 83, 4534 (1999). DOI:10.1103/PhysRevLett.83.4534
- ↑ Near-field optical manipulation by using evanescent waves
- ↑ Гл., напрыклад, K. Dholakia, Nature Materials 4, 579 —580 (01 Aug 2005) News and Views
- ↑ Burns M. M., Fournier J.-M., & Golovchenko J. A., «Optical binding», Phys. Rev. Lett. 63, 1233 (1989). DOI:10.1103/PhysRevLett.63.1233
- ↑ Pralle A. et al., «Three-Dimensional High-Resolution Particle Tracking for Optical Tweezers by Forward Scattered Light» Microscopy research and technique 44, 378 (1999). [5]
- ↑ Simmons R. M. et al., Biophysical Journal 70, 1813 (1996) Архівавана 29 сакавіка 2006.
- ↑ Schmitz C., Spatz J., & Curtis J., «High-precision steering of multiple holographic optical traps» Optics Express, 13, 8678 (2005). [6]
- ↑ Performance of optical traps with geometric aberrations by Y. Roichman et al., New York University
- ↑ Polin M. et al., Optics Express, 13, 5831 (2005)
- ↑ Optical Tweezers Архівавана 27 красавіка 2006.
Камерцыйныя сістэмы аптычных пінцэтаў[правіць | правіць зыходнік]
- Arryx Архівавана 6 снежня 2005.
- Cell Robotics
- Elliot Scientific
- MMI Molecular Machines & Industries
- PALM Архівавана 23 студзеня 2003.
Спасылкі[правіць | правіць зыходнік]
- Как работает оптический нанопинцет Архівавана 3 мая 2008. Богданов К. Ю. http://www.nanometer.ru/ Архівавана 24 жніўня 2013.
- Оптика биологических систем
Гэты артыкул уваходзіць у лік добрых артыкулаў беларускамоўнага раздзела Вікіпедыі. |












![{\displaystyle \mathbf {F} =\left(\mathbf {p} \cdot \nabla \right)\mathbf {E} +{\frac {d\mathbf {p} }{dt}}\times \mathbf {B} =\alpha \left[\left(\mathbf {E} \cdot \nabla \right)\mathbf {E} +{\frac {d\mathbf {E} }{dt}}\times \mathbf {B} \right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcf9c39cc75837d012b835056d4ab0649e212b55)




![{\displaystyle \mathbf {F} =\alpha \left[{\frac {1}{2}}\nabla E^{2}+{\frac {d}{dt}}\left(\mathbf {E} \times \mathbf {B} \right)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4c54d9ad6848d62c8bd9820e0e1b890b84279e2)
