Арыфметыка

Арыфме́тыка (стар.-грэч.: ἀριθμητική ад ἀριθμός — лік) — раздзел матэматыкі, які вывучае лікі, іх адносіны і ўласцівасці. Прадметам арыфметыкі з’яўляецца паняцце ліку ў развіцці ўяўленняў аб ім (натуральныя, цэлыя і рацыянальныя, рэчаісныя, камплексныя лікі) і яго ўласцівасцях. У арыфметыцы разглядаюцца вымярэнні, вылічальныя аперацыі (складанне, адніманне, множанне, дзяленне) і прыёмы вылічэнняў. Вывучэннем уласцівасцей асобных цэлых лікаў займаецца вышэйшая арыфметыка, ці тэорыя лікаў. Тэарэтычная арыфметыка надае ўвагу азначэнню і аналізу паняцця ліку, тады як фармальная арыфметыка аперуе лагічнымі пабудовамі прэдыкатаў і аксіём. Арыфметыка — найстаражытнейшая і адна з асноўных матэматычных навук, яна цесна звязана з алгебрай, геаметрыяй і тэорыяй лікаў[1][2].
Прычынай узнікнення арыфметыкі стала практычная патрэба ў лічэнні, найпрасцейшых вымярэннях і вылічэннях. Навука развівалася разам з ростам складанасці задач, якія патрабавалі рашэння. Вялікі ўклад у развіццё арыфметыкі ўнеслі грэчаскія матэматыкі, у тым ліку філосафы-піфагарэйцы, якія спрабавалі з дапамогай лікаў спасцігнуць і апісаць усе заканамернасці свету.
У Сярэднія вякі арыфметыку адносілі, услед за неаплатонікамі, да так званых Сямі вольных мастацтваў. Асноўнымі абласцямі практычнага прымянення арыфметыкі тады былі гандаль, навігацыя, будаўніцтва. У сувязі з гэтым асаблівае значэнне атрымалі прыбліжаныя вылічэнні ірацыянальных лікаў, неабходныя ў першую чаргу для геаметрычных пабудоў. Асабліва бурна арыфметыка развівалася ў Індыі і краінах ісламу, адкуль навейшыя дасягненні матэматычнай думкі праніклі ў Заходнюю Еўропу.
З надыходам Новага часу мараходная астраномія, механіка, больш складаныя камерцыйныя разлікі паставілі новыя запросы да тэхнікі вылічэнняў і падштурхнулі да далейшага развіцця арыфметыкі. У пачатку XVII ст. Непер вынайшаў лагарыфмы, а затым Ферма выдзеліў тэорыю лікаў у самастойны раздзел арыфметыкі. К канцу стагоддзя сфарміравалася ўяўленне аб ірацыянальным ліку як аб паслядоўнасці рацыянальных прыбліжэнняў, а на працягу наступнага стагоддзя дзякуючы працам Ламберта, Эйлера, Гауса арыфметыка ўключыла ў сябе аперацыі з камплекснымі велічынямі, набыўшы сучаснае аблічча.
Наступная гісторыя арыфметыкі адзначана крытычным пераглядам яе асноў, спробамі яе дэдуктыўнага абгрунтавання. Тэарэтычныя абгрунтаванні ўяўлення аб ліку звязаныя ў першую чаргу са строгім азначэннем натуральнага ліку і аксіёмамі Пеана, сфармуляванымі ў 1889 годзе. Несупярэчлівасць фармальнай пабудовы арыфметыкі была паказана Генценам у 1936 годзе.
Асновам арыфметыкі здаўна і нязменна надаецца вялікая ўвага ў пачатковай школьнай адукацыі.
Прадмет арыфметыкі[правіць | правіць зыходнік]

Прадметам арыфметыкі з’яўляюцца лікавыя мноствы, уласцівасці лікаў і дзеянні над лікамі[3]. Да яе таксама адносяць пытанні, звязаныя з тэхнікай лічэння, вымярэннямі[4], паходжаннем і развіццём паняцця ліку[1]. Арыфметыка вывучае натуральныя і рацыянальныя лікі, ці дробы[5]. На аснове аксіяматычнай структуры мноства натуральных лікаў ажыццяўляецца пабудова іншых лікавых мностваў, уключаючы цэлыя, рэчаісныя і камплексныя лікі, праводзіцца іх аналіз[1]. Часам у рамках арыфметыкі разглядаюць таксама кватэрніёны і іншыя гіперкамплексныя лікі. Разам з тым з тэарэмы Фрабеніуса вынікае, што пашырыць паняцце ліку за граніцы камплекснай плоскасці без страты нейкіх яго арыфметычных уласцівасцей немагчыма[6][7].
Да асноўных дзеянняў над лікамі адносяць складанне, адніманне, множанне і дзяленне[3], радзей узвядзенне ў ступень, здабыванне кораня[4] і рашэнне лікавых ураўненняў[3]. Гістарычна спіс арыфметычных дзеянняў таксама ўключаў уласна лічэнне, падваенне (акрамя множання), дзяленне на два і дзяленне з астачай (акрамя дзялення), пошук сумы арыфметычнай і геаметрычнай прагрэсій[8]. Непер у сваёй кнізе «Лагістычнае мастацтва» раздзяліў арыфметычныя дзеянні па ступенях. На самай нізкай ступені знаходзяцца складанне і адніманне, на наступнай — множанне і дзяленне, далей — узвяздзенне ў ступень і здабыванне каранёў[9]. Вядомы метадыст І. У. Арнольд да аперацый трэцяй ступені адносіў таксама лагарыфмаванне[10]. Традыцыйна арыфметыкай называюць выкананне аперацый над рознымі аб’ектамі, як то: «арыфметыка квадратычных форм», «арыфметыка матрыц»[1].
Уласна матэматычная разлікі і вымярэнні, неабходныя для практычных патрэб, як то: прапорцыі, працэнты, трайное правіла, адносяць да ніжэйшай ці практычнай арыфметыкі[3], тады як лагічны аналіз паняцця ліку адносяць да тэарэтычнай арыфметыкі[1]. Уласцівасці цэлых лікаў, дзяленне іх на часткі, пабудова непарыўных дробаў уваходзяць у тэорыю лікаў[1], якую доўгі час лічылі вышэйшай арыфметыкай[3]. Арыфметыка таксама цесна звязана з алгебрай, якая вывучае ўласна аперацыі без уліку асаблівасцей і ўласцівасцей лікаў[1][5]. Такія арыфметычныя дзеянні, як узвядзенне ў ступень і здабыванне каранёў, з’яўляюцца тэхнічнай часткай алгебры. У гэтым ключы, услед за Ньютанам і Гаусам, алгебру прынята лічыць абагульненнем арыфметыкі[3][4]. Увогуле кажучы, выразных граніц паміж арыфметыкай, элементарнай алгебрай і тэорыяй лікаў не існуе. У ВСЭ сказана: «Алгебра вывучае, карыстаючыся літарнымі абазначэннямі, агульныя ўласцівасці лікавых сістэм і агульныя метады рашэння задач пры дапамозе ўраўненняў; арыфметыка займаецца прыёмамі вылічэнняў з канкрэтна зададзенымі лікамі, а ў сваіх больш высокіх абласцях (гл. Лікаў тэорыя) — больш тонкімі індывідуальнымі ўласцівасцямі лікаў»[11].
Як і іншыя акадэмічныя дысцыпліны, арыфметыка сутыкаецца з прынцыповымі метадалагічнымі праблемамі; для яе неабходна даследаванне пытанняў несупярэчлівасці і паўнаты аксіём[3]. Лагічнымі пабудовамі фармальнай сістэмы прэдыкатаў і аксіём арыфметыкі займаецца фармальная арыфметыка[2].
Найпрасцейшыя паняцці[правіць | правіць зыходнік]
| Арыфметычныя аперацыі | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
Парадкавае лічэнне, натуральныя лікі[правіць | правіць зыходнік]

Самым простым арыфметычным паняццем з’яўляецца парадкавае лічэнне. Аб’ектам лічэння служацб розныя элементы ці іх мноствы, напрыклад: яблыкі і кошыкі яблыкаў. З дапамогай парадкавага лічэння можна пранумараваць элементы і абазначыць іх агульную колькасць.
Парадкавае лічэнне звязана з лічэннем групамі, якія ўтрымліваюць пэўную роўную колькасць элементаў, — напрыклад, лічэнне дзясяткамі яблыкаў. Звычайна гэта пальцы на дзвюх руках (аснова роўная ), але ў гістарычных крыніцах сустракаюцца групоўкі па . Колькасць элементаў у групе служаць асновай для сістэмы злічэння[5].
Лікавы рад, які атрымліваецца пры лічэнні, называюць натуральным, а яго элементы — натуральнымі лікамі. Паняцце натуральнага рада ўпершыню паявілася ў працах грэчаскага матэматыка Нікамаха ў I ст. н. э., а натуральнага ліку — у рымскага аўтара Баэцыя ў канцы V — пачатку VI ст. Усеагульнае ўжыванне тэрміна пачынаецца з работ Д’Аламбера ў XVIII ст. Архімед у сваёй рабоце «Псаміт» адзначыў, што лікавы рад можна працягваць неабмежавана, але разам з тым заўважыў, што для рэальных задач дастаткова невялікага адрэзка[12]. Дзяленне натуральных лікаў на цотныя і няцотныя прыпісваюць піфагарэйцам, яно таксама ёсць у егіпецкім папірусе Рында. Піфагарэйцы таксама вызначылі простыя і састаўныя лікі[13].
Складанне, множенне, узвядзенне ў ступень[правіць | правіць зыходнік]

Для натуральных лікаў натуральным чынам вызначаны аперацыі складання і множання. Пры аб’яднанні двух набораў, якія ўтрымліваюць некаторую колькасць прадметаў, новы набор будзе мець столькі прадметаў, колькі было ў першых двух наборах разам. Калі першы набор утрымліваў прадметы, а другі — прадметы, то іх сума будзе ўтрымліваць прадметаў. Апісанае дзеянне носіць назву складання і з’яўляецца найпрасцейшай бінарнай аперацыяй[4]. Для праверкі карэктнасці сумы табліцу складання знаць не абавязкова, досыць пералічыць прадметы[14].
Шматкратнае складанне элементаў некалькіх аднолькавых мностваз не залежыць ад парадку гэтых мностваў, што дазволіла вызначыць другую бінарную аперацыю — множанне[4]. Акрамя множання, у старажытнасці выдзялялася асобнае арыфметычнае дзеянне — падваенне, ці множанне на два[15].
Па аналогіі з вызначэннем множання цераз складанне, многаразовае множанне дазваляе вызначыць аперацыю ўзвядзення ў ступень.
Асноўныя законы арыфметыкі[правіць | правіць зыходнік]

Пра ўласцівасці гэтых аперацый сфармуляваны пяць законаў, якія лічацца асноўнымі законамі арыфметыкі[16]:
- Камутатыўнасць: перамяшчальны закон складання гаворыць, што ад змены месцаў складнікаў сума не мяняецца. Аналагічны закон вядомы і для множання, але ён, канечне, гаворыць аб множніках і здабытку. Гэтыя законы можна выразіць у алгебраічнай форме з дапамогай літарных абазначэнняў:
- Асацыятыўнасць: спалучальны закон складання гаворыць, што складваючы некалькі складнікаў, можна групаваць іх у любым парадку. Аналагічны закон для множання гаворыць аб перамнажэнні множнікаў. Гэтыя законы таксама можна запісаць у алгебраічнай форме:
- Дыстрыбутыўнасць: размеркавальны закон кажа: каб памножыць суму на лік, можна памножыць кожны складнік на гэты лік і потым скласці атрыманыя здабыткі. У алгебраічнай форме:
Акрамя асноўных законаў арыфметыкі для натуральных лікаў выконваюцца таксама законы манатоннасці складання і множання[17][18], якія ў алгебраічнай форме запісваюцца так:
- пры ;
- пры і .
Тэрмін «камутатыўны» для перамяшчальнага закона ўвёў у 1814 годзе французскі матэматык Сервуа. Тэрмін «асацыятыўны» для спалучальнага закона ўвёў у 1853 годзе Гамільтан[16].
Пуанкарэ разглядаў усе арыфметычныя аперацыі і законы з погляду інтуіцыі. Сцвярджаючы, што законы відавочным чынам выконваюцца для малых лікаў, і выкарыстоўваючы правіла індукцыі, можна прыйсці да вываду, што яны выконваюцца для ўсіх лікаў. Пры іншым падыходзе інтуітыўна вернымі лічацца не ўсе, а толькі самыя простыя законы, тады як далейшы доказ звязаны з лагічнымі пабудовамі[19]. За відавочныя прынімаліся перамяшчальны і спалучальны законы[16]. Размеркавальны, ці дыстрыбутыўны, закон у сваіх «Пачатках» доказваў яшчэ Еўклід, карыстаючыся геаметрычным метадам[20].
Аперацыя ўзвядзення ў ступень ужо не камутатыўныя і не асацыятыўная, у яе свае правілы. Асноўныя правілы выканання гэтай аперацыі пры дадатных ступенях відавочным чынам вынікаюць з яе азначэння[4]. У алгебраічнай форме іх можна запісаць наступным чынам:
- Дыстрыбутыўнасць: размеркавальны закон для аперацыі ўзвядзення ў ступень:
-
- ён жа, у выпадку аднімання, набывае форму дробу:
- Паўторнае ўзвядзенне ў ступень раскрываецца як перамнажэнне ступеней:
- .
Адваротныя аперацыі[правіць | правіць зыходнік]
Ва ўсіх аперацый арыфметыкі ёсць адваротныя: у складання — адніманне, у множання — дзяленне, ва ўзвядзення ў ступень — арыфметычны корань і лагарыфм. Тое, што ў складання і множання па адной адваротнай аперацыі, нягледзячы на іх бінарнасць, тлумачыцца іх камутатыўнасцю.
Адніманне: адмоўныя лікі[правіць | правіць зыходнік]

Адніманне — гэта аперацыя, адваротная складанню: рознасцю двух лікаў і з’яўляецца невядомая з ураўнення [4]. Абазначаецца аперацыя аднімання знакам «−» і запісваецца ў выглядзе . Для выканання аперацыі прымянялі два прыёмы: адлічванне ад памяншаемага ліку адзінак аднімаемага ці падбор такога ліку, прыбаўленне якога да аднімаемага давала бы памяншаемае[15].
Аперацыя аднімання, калі яе прымяняць да ўсіх пар натуральных лікаў, а не толькі да такіх, якія маглі б быць сумай і складнікам у рамках аперацыі складання, дазваляе выйсці за граніцы натуральнага рада, г.зн. рознасць двух натуральных лікаў не абавязкова будзе натуральным лікам — у выніку аднімання можа атрымацца нуль ці ўвогуле адмоўны лік. Адмоўныя лікі ўжо немагчыма разглядаць як колькасць прадметаў, на лікавай восі яны размяшчаюцца злева ад нуля. Мноства лікаў, атрыманае дабаўленнем да натуральных лікаў адмоўных лікаў і ліку нуль, носіць назву мноства цэлых лікаў. Нуль і мноства натуральных лікаў называюцца дадатныя цэлыя лікі[4]. Пры множанні, каб вызначыць, дадатным ці адмоўным будзе здабытак лікаў, карыстаюцца «правілам знакаў»[21].
Адмоўныя лікі лічылі несапраўднымі і бессэнсоўнымі вельмі многія матэматыкі аж да XIX ст., што, аднак, не замінала іх паўсюднаму фармальнаму ўжыванню. Упершыню паняцце адмоўных лікаў паявілася ў Індыі, дзе іх тлумачылі як «доўг» (дадатныя лікі — «маёмасць»). Распаўсюдзіліся ж адмоўныя лікі толькі ў XVII ст.[22] Тэрмін «адніманне» паявіўся яшчэ ў Баэцыя, тэрміны «аднімаемае» і «памяншаемае» ўвёў ва ўжытак Вольф у 1716 годзе, «рознасць» — Відман у 1489 годзе[15]. Сучасныя абазначэнні знакамі «+» і «−» таксама ўвёў Відман у канцы XV ст.
Дзяленне: рацыянальныя лікі[правіць | правіць зыходнік]

Адваротнай да аперацыі множання з’яўляецца аперацыя дзялення. Першае вызначэнне дзялення — гэта пошук ліку, які ўтрымліваецца ў дзялімым столькі разоў, колькі адзінак утрымліваецца ў дзельніку. Такое азначэнне дадзена ў падручніках арыфметыкі XIV ст. Напрыклад, . Дзяленне лічылася вельмі складанай і грувасткай аперацыяй. Сучасны спосаб дзялення, які выкарыстоўвае частковыя здабыткі дзельніка на асобныя разрады дзелі (дзяленне слупком), прадстаўлен у італьянскім рукапісе 1460 года[15].
Для натуральных лікаў, якія не з’яўляюцца множнікам і здабыткам, вядома аперацыя дзяленне з астачай (а азначэнне ўласна астачы ад дзялення таксама называецца дзяленне па модулю). Таксама існуе мноства спосабаў, якія спрашчаюць дзяленне ў розных асобных выпадках ці дазваляюць праверыць дзялімасць на той ці іншы лік. Напрыклад:
- лік без астачы дзеліцца на два, калі яго апошняя лічба ў дзесятковым запісе дзеліцца на два;
- лік без астачы дзеліцца на тры, калі сума ўсіх яго лічбаў у дзесятковым запісе дзеліцца на тры;
- лік без астачы дзеліцца на дзесяць, калі яго апошняя лічба ў дзесятковым запісе — нуль.
Аперацыя дзялення, калі дзяліць не толькі тыя лікі, якія можна атрымаць множаннем натуральных лікаў, і пры гэтым не выдзяляць астатак, таксама як і адніманне, дазваляе выйсці за граніцы мноства натуральных лікаў. Пры дзяленні могуць атрымацца дробы, якія немагчыма без астачы скараціць да цэлага. Лікі, якія адпавядаюць такім дробам, называюцца рацыянальнымі. За кошт усведамлення заснаваных на дзяленні рацыянальных лікаў адбываецца яшчэ адно пашырэнне набору вядомых відаў лікаў. Гістарычна спачатку ўзнікла паняцце дробу, а затым адмоўнага ліку[23]. Такі ж парадак прыняты ў школьным курсе[24].
Ужываецца дзве формы запісу дробаў — у выглядзе лічніка і назоўніка, раздзеленых гарызантальнай ці нахіленай рысай і часта скарочаных да ўзаемна простых лікаў, і ў выглядзе лічбаў дробнай часткі, размешчаных пасля знака-раздзяляльніка цэлай і дробнай часткі ў пазіцыйнага запісу ліку. Напрыклад, вынік дзялення 10 на 20 можна запісаць як .
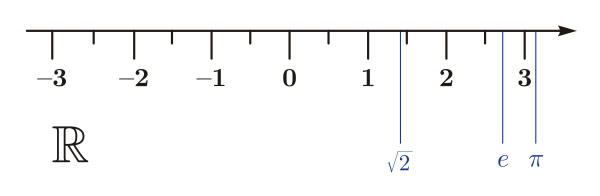
Узяцце кораня: ірацыянальныя і камплексныя лікі[правіць | правіць зыходнік]
Адна з дзвюх адваротных для ўзвядзення ў ступень аперацый — узяцце кораня. Гэта пошук ліку, які пры ўзвядзенні ў адпаведную ступень будзе даваць вядомы вынік. Г.зн. кажучы алгебраічна, гэта пошук кораня для ўраўнення віду . Другая адваротная аперацыя — лагарыфм, гэта корань ураўнення віду . Да арыфметыкі, як правіла, адносяць толькі вылічэнне кораня другой ступені — квадратнага кораня. Карані іншых ступеней і лагарыфмы арыфметычнымі аперацыямі не лічацца.
Аперацыя вылічэння кораня, калі выконваць яе не толькі для тых лікаў, якія можна атрымаць узвядзеннем у ступень натуральных лікаў, таксама як і астатнія адваротныя аперацыі, дазваляе выйсці за граніцы мноства натуральных лікаў. Лікі, якія атрымліваюцца пры гэтым, часта нельга прадставіць у выглядзе канечных рацыянальных дробаў, і таму яны называюцца ірацыянальнымі. Мноства лікаў, атрыманае дабаўленнем к рацыянальным лікам ірацыянальных, назвалі рэчаіснымі, ці сапраўднымі лікамі.
Яшчэ ў Старажытнай Грэцыі было вядома пра існаванне несувымерных адрэзкаў, прынамсі, на прыкладзе старон і дыяганалі квадрата са стараной, прынятай за адзінку, і ажыццяўляліся спробы атрымаць для іх дакладныя лікавыя значэнні, што знайшло адлюстраванне ў «Пачатках» Эўкліда. Рэчаісныя лікі сталі аб’ектам даследаванняў толькі ў XVII—XVIII ст. У другой палавіне XIX ст. Дэдэкінд, Кантар і Веерштрас сфармулявалі свае канструктыўныя спосабы азначэння рэчаіснага ліку[25].
Для аперацыі здабывання кораня вядома наступнае правіла[4]:
Далейшае пашырэнне мноства лікаў было звязана з немагчымасцю здабыцця квадратнага кораня з адмоўнага ліку. З падобнай задачай сутыкаліся ў старажытнасці пры рашэнні квадратных ураўненняў, і такія ўраўненні проста лічылі невырашальнымі. У першай палавіне XVI ст. сталі выражаць рашэнні такіх ураўненняў цераз карані з адмоўных лікаў і называць такія карані «уяўнымі», «немагчымымі» і т. д.[26]
Практычная арыфметыка[правіць | правіць зыходнік]
Практычны бок арыфметыкі ўключае ў сябе метады, схемы і алгарытмы для ажыццяўлення дакладных арыфметычных дзеянняў, у тым ліку выкарыстанне лічыльных машын і іншых прылад, а таксама розныя прыёмы прыбліжаных вылічэнняў, якія з’явіліся ад немагчымасці атрымаць дакладны вынік пры некаторых вымярэннях і дазваляюць вызначыць яго парадак, г.зн. першыя значныя лічбы[27].
- Найпрасцейшыя лічыльныя прылады
-
Рускія шчоты (лічыльнікі)
Дакладныя метады[правіць | правіць зыходнік]
Пачынаючы з XV ст. прапаноўваліся розныя алгарытмы для ажыццяўлення арыфметычных аперацый над многаразраднымі лікамі, якія адрозніваюцца характарам запісу прамежкавых вылічэнняў[1]. Арыфметычныя алгарытмы пабудаваны на ўжываемай пазіцыйнай сістэме злічэння, калі любы дадатны рэчаісны лік адназначна запісваецца ў выглядзе
дзе — чарговая лічба запісу ліку , — аснова сістэмы злічэння, — колькасць разрадаў цэлай часткі ліку .
Усе дзеянні над лікамі грунтуюцца на табліцах складання і множання да дзесяці і асноўных арыфметычных законах. У якасці ілюстрацыі вядомы папулярызатар навукі Клейн прыводзіць наступны прыклад:
у якім выкарыстоўваюцца размеркаваны і спалучальны законы[28].
Патрэба ў быстрых і дакладных вылічэннях прывяла да стварэння найпрасцейшых лічыльных прылад: абака, суаньпаня, юпаны ці лічыльнікаў (шчотаў). Наступным крокам было стварэнне Оўтрэдам у 1622 годзе лагарыфмічнай лінейкі, якая дазваляе ажыццяўляць множанне і дзяленне[29].
Камп’ютарная арыфметыка[правіць | правіць зыходнік]

Кнут лічыў арыфметычныя дзеянні «удзелам камп’ютараў»[30]. Першыя вылічальныя машыны, якія дазвалялі механізаваць чатыры арыфметычныя дзеянні, былі сканструяваны ў XVII ст. «Арыфметычная машына» Шыкарда, як ён сам яе называў, была пабудавана ў 1623 годзе. Аперацыі складання і аднімання праводзіліся шляхам кручэння цыліндраў, спецыяльныя цыліндры былі таксама для множання і дзялення. Акрамя таго, машына магла пераносіць дзясяткі. Машына Паскаля была распрацавана ім у 1642 годзе ў помач бацьку ў выкананні фінансавых разлікаў. Яна мела той жа прынцып дзеяння, што і машына Шыкарда. Асноўную частку машыны складаў механізм пераносу дзясяткаў. Разам з тым рамесны выраб такіх машын усё яшчэ заставалася нявыгадным[31]. Спробы ўдасканаліць арыфмометр працягваліся ўсё XVIII стагоддзе, але толькі ў XIX ст. ужыванне арыфмометраў набыло шырокую распаўсюджанасць[32].
У XX ст. на змену арыфмометрам прыйшлі электронныя вылічальныя машыны. У іх аснове ляжаць алгарытмы, якія выкарыстоўваюць найменшы лік элементарных аперацый для выканання арыфметычных дзеянняў[1]. Камп’ютарная арыфметыка ўключае алгарытмы выканання аперацый над лікамі з плаваючай коскай, дробамі і вельмі вялікімі лікамі[30].
Вымярэнне[правіць | правіць зыходнік]
Акрамя прадметаў, якія можна пералічыць, існуюць прадметы, якія можна вымераць, у першую чаргу гэта даўжыня і маса[33]. Як і пры лічэнні, першымі мерамі даўжыні ў чалавека былі пальцы рук. Затым адлегласць сталі мераць крокамі, двайнымі крокамі, мілямі (тысяча двайных крокамі), стадыямі. Акрамя таго, для вымярэння даўжыні выкарыстоўвалі локці, далоні, сажні, дзюймы. У розных рэгіёнах устанаўліваліся свае сістэмы мер, якія рэдка былі кратныя дзесяці[34]. Мнагастайнасць мер, в прыватнасці, дазваляла абысціся без выкарыстання дробаў[35][36]. Тарговая арыфметыка ўключала ў сябе ўменне аперыраваць велічынямі (грашовымі адзінкамі, адзінкамі мер і вагаў) у недзесятковай сістэме злічэння[37].
У канцы XVIII ст. французскім рэвалюцыйным урадам на аснове часовага — а затым і архіўнага (законам 10 снежня 1799 года) — метра была прынята метрычная сістэма мер (канчаткова Францыя перайшла на яе з 1 студзеня 1840 года). Разам з метрам быў вызначан і кілаграм. У аснове метрычнай сістэмы ляжыць дзесятковая сістэма. Іменна гэтая акалічнасць дазволіла метрычнай сістэме распаўсюдзіцца амаль на ўвесь свет (выключэнне складаюць Вялікабрытанія і ЗША). Па ўказу спецыяльнага Міжнароднага бюро мер і вагаў, размешчанага ў Парыжы, у 1888 годзе са сплаву плаціны і ірыдыю былі зроблены міжнародны метр і міжнародны кілаграм — эталоны мер і вагаў. Акрамя мер часу і вугла, усе астатнія адзінкі мер таксама звязаныя з дзесятковай сістэмай[38].
Прыбліжаныя метады[правіць | правіць зыходнік]
Гістарычна прыбліжаныя вылічэнні ўзніклі пры пошуку даўжыні дыяганалі адзінкавага квадрата, але атрымалі шырокае распаўсюджанне пры пераходзе да дзесятковай сістэмы і выкарыстанні канечных дзесятковых дробаў замест ірацыянальных лікаў і лікаў, выражаных бесканечным перыядычным дробам[39].
Для ацэначных вылічэнняў выкарыстоўваюць, у першую чаргу, законы манатоннасці. Напрыклад, каб вызначыць парадак здабытку , можна выкарыстаць наступную ацэнку [28].
Тэорыя лікаў[правіць | правіць зыходнік]
Тэорыя лікаў, ці вышэйшая арыфметыка, — гэта навука аб цэлых ліках, якая ўзнікла з арыфметычных задач, звязаных з дзялімасцю лікаў[40]. Элементарная тэорыя лікаў мае справу з праблемамі, якія рашаюцца элементарнымі метадамі, звычайна без выкарыстання ўяўных лікаў. Да яе адносяць тэорыю дзялімасці, тэорыю параўнанняў, нявызначаныя ўраўненні, разбіццё на складнікі, прыбліжэнні рацыянальнымі лікамі, ланцуговыя дробы[41]. Асноўная тэарэма арыфметыкі — пра адназначнасць раскладання ліку на простыя множнікі — таксама з’яўляецца часткай элементарнай тэорыі лікаў[42].
Асобныя падкласы цэлых лікаў, такія як простыя, састаўныя, квадратныя, дасканалыя лікі, былі выдзелены яшчэ старажытнымі грэкамі. Яны вывелі формулы для вызначэння піфагоравых троек, найбольшага агульнага дзельніка, паказалі бесканечнасць колькасці простых лікаў. Дыяфант правёў сістэматызацыю задач, звязаных з цэлымі лікамі. Работы Дыяфанта былі працягнуты Ферма ў XVII і Эйлерам у XVIII ст. Ферма займаўся рашэннем ураўненняў у цэлых ліках і сфармуляваў без доказу малую і вялікую тэарэмы Ферма. Эйлер, працягваючы даследаванні Ферма, даказаў малую тэарэму і асобны выпадак вялікай тэарэмы Ферма. Ён упершыню прымяніў матэматычны аналіз для рашэння задач тэорыі лікаў і стварыў аналітычную тэорыю лікаў. Эйлер вызначыў утваральныя функцыі, на аснове якіх былі пабудаваныя кругавы метад і метад трыганаметрычных сум[40].
Цяпер, акрамя элементарнай і аналітычнай тэорыі лікаў, існуюць такія раздзелы, як адытыўная, алгебраічная, імавернасная, метрычная тэорыя лікаў[40].
Тэарэтычная арыфметыка[правіць | правіць зыходнік]
У сучаснай матэматыцы пабудова тэорыі прадстаўляе сабой выбар базавых уласцівасцей, ці аксіём, з якіх патрабуецца вывесці ўсе палажэнні тэорыі, ці тэарэмы, з дапамогай агульнапрынятай логікі[43]. Тэарэтычная пабудова арыфметыкі аперыруе алгебраічнымі паняццямі. Складанасць выдзялення асноўных азначэнняў арыфметыкі звязана з простасцю яе начальных палажэнняў. Пеана, асцерагаючыся памылковага асацыятыўнага рада пры выкарыстанні слоў, праводзіў доказы выключна на мове сімвалаў, абапіраючыся толькі на прынятыя ім папярэднія палажэнні. Кантар і Дэдэкінд звязалі лікі з мноствамі і абстрактнымі адносінамі над імі[19]. Тэорыя мностваў разглядае арыфметычныя дзеянні як асаблівыя адносіны паміж тройкамі элементаў, у якіх адзін элемент вызначаецца цераз два іншыя, ці алгебраічныя аперацыі[44]. Кажучы пра тэорыю мностваў, Клейн заўважыў, што пры такім падыходзе развіццё тэорыі становіцца «адцягнутым і мала даступным»[19].
Натуральныя лікі[правіць | правіць зыходнік]
У 1810 годзе чэшскі матэматык Бальцана вызначыў дзеянне складання для натуральных лікаў. Незалежна ад яго падобнае азначэнне далі нямецкія матэматыкі Грасман у 1861 годзе і Ганкель у 1869 годзе[45]. «Энциклопедия элементарной математики» прапануе наступнае азначэнне складання натуральных лікаў[46]:
|
Азначэнне. Складеннем натуральных лікаў называецца такая адпаведнасць, якая кожнай пары натуральных лікаў і супастаўляе адзін і толькі адзін натуральны лік і валодае наступнымі ўласцівасцямі:
|
Складанне натуральных лікаў заўсёды ажыццявімае і адназначнае[46].
Множанне, як і складанне, вызначылі незалежна Бальцана, Грасман і Ганкель[45]. «Энциклопедия элементарной математики» прапануе наступнае азначэнне множання натуральных лікаў[47]:
|
Азначэнне. Множаннем натуральных лікаў называецца такая адпаведнасць, якая кожнай пары натуральных лікаў і супастаўляе адзін і толькі адзін натуральны лік (ці ) і валодае наступнымі ўласцівасцямі:
|
Множанне натуральных лікаў заўсёды ажыццявімае і адназначнае[47].
У 1891 годзе Пеана прадставіў аксіёмы для натуральных лікаў (у іншых крыніцах упамінаецца таксама 1889 год)[5][45]. З тае пары аксіёмы змяніліся вельмі нязначна.
|
Азначэнне. Натуральнымі лікамі называюцца элементы ўсякага непустога мноства , у яком для некаторых элементаў і існуе дачыненне « ідзе за », для якога выконваюцца наступныя аксіёмы[48]:
|
Цэлыя лікі[правіць | правіць зыходнік]
«Энциклопедия элементарной математики» прапануе наступнае азначэнне аднімання натуральных лікаў[49]:
|
Азначэнне. Адніманнем натуральных лікаў называецца такая адпаведнасць, якая кожнай пары натуральных лікаў і супастаўляе лік з наступнай уласцівасцю:
|
Адніманне натуральных лікаў ажыццявіма, толькі калі , калі рознасць існуе, то яна адназначная[49]. Пашырэнне натуральных лікаў за кошт уласцівасцей складання і аднімання прыводзіць да паняцця цэлых лікаў[50].
|
Азначэнне. Кальцом цэлых лікаў называецца мінімальнае кальцо , якое ўтрымлівае мноства усіх натуральных лікаў і валодае наступнымі ўласцівасцямі[51]:
Элементы кальца называюцца цэлымі лікамі. |
Кальцо існуе і з’яўляецца адзіным з дакладнасцю да ізамарфізма, а кожны яго элемент ровен рознасці натуральных лікаў. Пры пабудове кальца выкарыстоўваюць мноства пар натуральных лікаў віду . Для пар вызначаюць эквівалентнасць, складанне і множанне наступным чынам[51]:
- эквівалентна тады і толькі тады, калі
Рацыянальныя лікі[правіць | правіць зыходнік]
«Энциклопедия элементарной математики» прапануе наступнае азначэнне дзялення натуральных лікаў[49]:
|
Азначэнне. Дзяленнем натуральных лікаў называецца такая адпаведнасць, якая кожнай пары натуральных лікаў і супастаўляе лік і валодае наступнай уласцівасцю:
|
Дзяленне натуральных лікаў ажыццявіма, толькі калі ( кратна ), калі дзель існуе, то яна адзіная[49]. Пашырэнне цэлых лікаў за кошт паняццяў множання і дзялення прыводзіць да азначэння рацыянальных лікаў[50]. Яшчэ ў 1710 годзе Вольф выказаў патрабаванне, што ўжо вядомыя законы выканання арыфметычных дзеянняў з цэлымі лікамі не могуць напрамую прымяняцца для дробаў і павінны быць абгрунтаваны. Сама абгрунтаванне было распрацавана толькі ў XIX ст. з выкарыстаннем прынцыпа пастаянства фармальных законаў[52].
|
Азначэнне. Полем рацыянальных лікаў называецца мінімальнае поле , якое ўтрымлівае кальцо цэлых лікаў і валодае наступнымі ўласцівасцямі[24]:
Элементы поля называюцца рацыянальнымі лікамі. |
Поле існуе і з’яўляецца адзіным з дакладнасцю да ізамарфізма, а кожны яго элемент ровен дзелі цэлых лікаў. Як і для цэлых лікаў, пры пабудове поля рацыянальных лікаў выкарыстоўваюць мноства пар , але цяпер ужо цэлых лікаў, пры гэтым . Для пар вызначаюць эквівалентнасць, складанне і множанне наступным чынам[24]:
- эквівалентна тады і толькі тады, калі
Рэчаісныя лікі[правіць | правіць зыходнік]
У другой палавіне XIX ст. было прапанавана тры розныя тэарэтычныя пабудовы сапраўдных лікаў. Найбольш папулярнай з’яўляецца пабудова Дэдэкінда. Кантар у сваёй пабудове выкарыстоўваў тэорыю граніц[53].
|
Азначэнне. Полем рэчаісных лікаў называецца непарыўнае поле , якое ўтрымлівае ў якасці падполя поле рацыянальных лікаў. Элементы поля называюцца рэчаіснымі лікамі[54]. |
Поле існуе і з’яўляецца адзіным з дакладнасцю да ізамарфізма, а кожны яго элемент ровен граніцы паслядоўнасці рацыянальных лікаў[54].
Камплексныя лікі[правіць | правіць зыходнік]
|
Азначэнне. Полем камплексных лікаў называецца мінімальнае поле , якое ўтрымлівае поле рэчаісных лікаў і элемент такі, што , і валодае наступнымі ўласцівасцямі[55]:
Элементы поля называюцца камплекснымі лікамі. |
Поле з’яўляецца алгебраічна замкнутым. Пры пабудове поля камплексных лікаў выкарыстоўваецца мноства ўпарадкаваных пар . Для пар вызначаюць эквівалентнасць, складанне і множанне наступным чынам:
- эквівалентна тады і толькі тады, калі і ,
Фармальная арыфметыка[правіць | правіць зыходнік]
Логіка-матэматычная пабудова носіць назву фармальнай арыфметыкі[56]. Пераход да логікі звязан з падыходам школы Гільберта, які разглядаў замест лікаў абстракцыі і меркаваў для іх вернымі асноўныя арыфметычныя законы[19]. Для абгрунтавання арыфметыкі было прапанавана некалькі варыянтаў аксіяматыкі. Акрамя сістэмы аксіём Пеана, у якой вызначаныя і складанне, і множанне, існуе сістэма аксіём Прэсбургера, у якой вызначана толькі складанне, а таксама аксіёмы, у якіх вызначаны складанне, множанне і ўзвядзенне ў ступень. Часта ў якасці аксіём уключаюць усе ўласцівасці аперацый[57][58]. Усе гэтыя аксіяматычныя тэорыі заснаваныя на мностве цэлых лікаў і не ўключаюць у сябе парадоксы тэорыі мностваў. Іншыя даследчыя падыходы выводзяць арыфметыку з аксіём тэорыі мностваў або матэматычнай логікі[43]. Для зручнасці даследавання аксіёмы запісваюць на спецыяльнай фармальнай мове матэматычнай логікі[56]. Яна ўтрымлівае , лікавыя пераменныя, сімвалы () і лагічныя звязкі (), пастулатамі з’яўляюцца пастулаты прэдыкатаў злічэння[2]. Аксіёма індукцыі ўяўляе сабой бесканечны набор аксіём, які нельга замяніць ніякім канечным мноствам[56].
У ідэале базавы набор аксіём павінен валодаць трыма якасцямі[5]:
- Несупярэчлівасць — аксіёмы не павінны канфліктаваць адна з адной;
- Незалежнасць — сярод аксіём не павінна быць лішніх, якія лагічна выводзяцца з іншых аксіём;
- Паўната — набор аксіём павінен быць дастатковы для таго, каб любую правільна сфармуляваную тэарэму можна было даказаць ці абвергнуць.
Арыфметыка натуральных лікаў мае вялікае значэнне для абгрунтавання матэматычных тэорый: з яе несупярэчлівасці вынікае несупярэчлівасць арыфметыкі сапраўдных лікаў, якая ў сваю чаргу дазваляе, карыстаючыся метадам мадэлей, паказаць несупярэчлівасць эўклідавай геаметрыі і геаметрыі Лабачэўскага[5][43]. Доказам несупярэчлівасці арыфметыкі ў сістэме Пеана і роднасных ёй аксіяматычных сістэмах беспаспяхова займаўся Гільберт у пачатку XX стагоддзя. Пасля адкрыцця ў 1930 годзе тэарэмы Гёдэля аб непаўнаце стала ясна, што ў падобных простых сістэмах гэта немагчыма. Доказ несупярэчлівасці быў праведзены ў 1936 годзе Генцэнам з выкарыстаннем разнавіднасці трансфінітнай індукцыі[56].
Для даследавання незалежнасці кожная аксіёма па чарзе замяняецца на процілеглую і затым будуецца мадэль, дзе атрыманы набор аксіём выконваецца. Калі замененая аксіёма залежная, г.зн. лагічна выцякае з іншых аксіём, то замена яе на процілеглую, відавочна, прыводзіць да супярэчлівай сістэмы аксіём, і пабудова мадэлі немагчыма. Такім чынам, калі мадэль удаецца пабудаваць, то адпаведная аксіёма незалежная[59]. Такім спосабам было даказана, што ўсе аксіёмы Пеана незалежныя адна ад адной[60].
Сродкамі фармальнай арыфметыкі, якая будуецца на аксіёмах Пеана, можна запісаць тэарэмы тэорыі лікаў, якія даказваюцца без выкарыстання матэматычнага аналізу, а таксама рэкурсіўныя функцыі і іх уласцівасці[2]. Яна эквівалентная аксіяматычнай тэорыі мностваў Цэрмела — Фрэнкеля без аксіёмы бесканечнасці. Разам з тым даказаная ў 1929 годзе тэарэма Гёдэля аб паўнаце паказала, што аксіяматыка Пеана няпоўная, г.зн. існуюць арыфметычныя тэарэмы, якія нельга ні даказаць, ні абвергнуць. У той час як арыфметыка поўная адносна формул віду , існуюць тэарэмы віду , якія сцвярджаюць праўдзівы факт, але іх немагчыма вывесці[56]. Удалося знайсці і канкрэтныя прыклады тэарэм: тэарэма Гудстэйна, Тэарэма Пэрыса – Харынгтана і іншыя.
Гісторыя[правіць | правіць зыходнік]
Старажытныя матэматычныя тэксты і сістэмы злічэння[правіць | правіць зыходнік]

Егіпецкія матэматычныя тэксты асаблівую ўвагу надавалі вылічэнням і ўзнікаючым пры гэтым складанасцям, ад якіх у многім залежалі метады рашэння задач. Матэматычныя папірусы Старажытнага Егіпта былі састаўлены для навучальных мэт[61], яны ўтрымлівалі задачы з рашэннямі, дапаможныя табліцы і правілы дзеянняў над цэлымі лікамі і дробамі, сустракаюцца арыфметычныя і геаметрычныя прагрэсіі, а таксама ўраўненні[5]. Егіпцяне карысталіся дзесятковай сістэмай злічэння[62]. Егіпцяне зналі такія арыфметычныя аперацыі, як складанне, падваенне і дапаўненне дробу да адзінкі. Любое памнажэнне на цэлы лік і дзяленне без астачы праводзіліся з дапамогай шматразовага паўтарэння аперацыі падваення, што прыводзіла да грувасткіх вылічэнняў, у якіх удзельнічалі пэўныя члены паслядоўнасці [14]. У Егіпце знайшлі прымяненні толькі аліквотныя дробы, ці долі адзінкі (), а ўсе астатнія дробы раскладаліся на суму аліквотных[63]. Пры вызначэнні плошчы квадрата, аб’ёму куба ці знаходжанні стараны квадрата па яго плошчы егіпцяне сутыкаліся з узвядзеннем у ступень і здабываннем кораня, хаця назвы гэтым аперацыям яшчэ не было[14].

Вавілонскія клінапісныя матэматычныя тэксты выкарыстоўвалі шасцідзесятковую сістэму злічэння, характэрную яшчэ для шумераў[64], і прадстаўлялі сабой навучальныя дапаможнікі, якія ўключаюць табліцы множання для лікаў ад да , а таксама табліцы адваротных лікаў, табліцы квадратаў і кубоў лікаў натуральнага рада, табліцы вылічэння працэнтаў, дробы з асноваю [5][62]. Пры рашэнні арыфметычных задач вавіланяне апіраліся на прапорцыі і прагрэсіі. Яны зналі формулу сумы членаў арыфметычнай прагрэсіі, правіла для суміравання геаметрычнай прагрэсіі, рашалі задачы на працэнты[65]. У Вавілоне зналі мноства піфагоравых троек, для пошуку якіх, верагодна, карысталіся невядомым агульным прыёмам. У цэлым задача знаходжання цэлых і рацыянальных рашэнняў ураўнення адносіцца да тэорыі лікаў[66]. Геаметрычныя задачы прывялі да неабходнасці прыбліжанага здабывання квадратных каранёў, якія яны выконвалі, карыстаючыся правілам і ітэрацыйнымі метадамі для далейшага прыбліжэння выніку[ком. 1].

Найстаражытнейшыя грэчаскія матэматычныя тэксты адносяцца да XIV—VII ст. да н. э.[68] Першапачаткова грэкі карысталіся атычнай нумарацыяй, якую з часам замяніла кампактная літарная, ці іанічная[69]. Развіццё старажытнагрэчаскай арыфметыкі належыць піфагарэйскай школе. Піфагарэйцы меркавалі спачатку, што адносіну любых двух адрэзкаў можна выразіць цераз адносіну цэлых лікаў, г.зн. геаметрыя прадстаўляла сабой арыфметыку рацыянальных лікаў. Яны разглядалі толькі цэлыя дадатныя лікі і вызначалі лік як збор адзінак. Вывучаючы ўласцівасці лікаў, яны разбілі іх на цотныя і няцотныя (як прыкмета дзялімасці на два), простыя і састаўныя, знайшлі бесканечнае мноства піфагоравых троек[70]. У 399 годзе да н. э. з'явілася агульная тэорыя дзялімасці, якая належыць, відаць, Тээтэту, вучню Сакрата. Еўклід прысвяціў ёй кнігу VII i частку кнігі IX «Пачаткаў». У аснове тэорыі ляжыць алгарытм Еўкліда для знаходжання найбольшага агульнага дзельніка двух лікаў. З алгарытму вынікае той факт, што любы лік можна раскласці на простыя, прычым такое раскладанне адзінае[71].
Разам з тым піфагарэйцам належыць доказ несувымернасці дыяганалі і стараны адзінкавага квадрата. Дадзенае адкрыццё паказала, што адносін цэлых лікаў недастаткова для выражэння адносін любых адрэзкаў, і на гэтай аснове немагчыма будаваць метрычную геаметрыю[72]. Першае вучэнне аб ірацыянальнасцях належыць Тээтэту. Алгарытм Еўкліда дазваляе вызначыць няпоўныя дзелі раскладання рацыянальнага ліку ў непарыўны дроб. Разам з тым паняцце непарыўнага дробу ў Старажытнай Грэцыі не ўзнікла[71]. У III стагоддзі Дыяфант пачаў пабудову алгебры з апорай не на геаметрыю, а на арыфметыку. Дыяфант таксама пашырыў лікавую вобласць на адмоўныя лікі[73].
Рымская сістэма нумарацыі была мала прыстасаваная для вылічэнняў. Рымскія лічбавыя знакі ўзніклі да з'яўлення алфавіта і не паходзяць ад яго літар. Лічыцца, што першапачаткова лікі ад да абазначыліся адпаведнай колькасцю вертыкальных рысачак, а іх перакрэсліванне азначала ўдзесяцярэнне ліку (адсюль лік ). Адпаведна, каб атрымаць лік , палачку перакрэслівалі два разы. Пасля адбылося спрашчэнне сістэмы[74]. У цяперашні час яна ўжываецца ў асноўным для абазначэння парадкавых лікаў.
Да XIV стагоддзя матэматыка Кітая ўяўляла сабой набор вылічальных алгарытмаў для рашэння на лічыльнай дошцы[75]. Арыфметычныя аперацыі складання і аднімання, якія рабіліся на лічыльнай дошцы, не патрабавалі дадатковых табліц, для множання ж існавала табліца ад да . Дзеянні множання і дзялення рабіліся пачынаючы са старэйшых разрадаў, пры гэтым прамежкавыя вынікі выдаляліся з дошкі, што рабіла праверку немагчымай. Спачатку множанне і дзяленне былі незалежнымі аперацыямі, але затым Сунь Цзы адзначыў іх узаемную адваротнасць[76]. У Кітаі ўмелі рашаць задачы з дапамогай правілы двух ілжывых палажэнняў[77], а для рашэння сістэм лінейных ураўненняў былі ўведзеныя адмоўныя лікі. Спачатку яны выкарыстоўваліся толькі ў працэсе разлікаў і к канцу вылічэнняў выдаляліся з дошкі, затым кітайскія навукоўцы сталі тлумачыць іх як доўг або недастачу[78].
Арыфметыка ў Сярэдневякоўі[правіць | правіць зыходнік]

Пазіцыйная сістэма злічэння (дзесяць лічбаў, уключаючы нуль) была ўведзена ў Індыі. Яна дазволіла распрацаваць параўнальна простыя правілы выканання арыфметычных аперацый[5]. Асноўнымі арыфметычнымі дзеяннямі ў Індыі лічыліся складанне, адніманне, множанне, дзяленне, узвядзенне ў квадрат і куб, здабыванне квадратных і кубічных каранёў, для якіх былі распрацаваны правілы. Вылічэнні праводзіліся на лічыльнай дошцы з пяском ці пылам або проста на зямлі і запісваліся палачкай[79]. Індыйцы ведалі дробы і ўмелі здзяйсняць аперацыі над імі, прапорцыі, прагрэсіі[80]. Ужо з VII стагоддзя н. э. яны карысталіся адмоўнымі лікамі, інтэрпрэтуючы іх як доўг, а таксама ірацыянальнымі лікамі[81].

У пачатку IX стагоддзя Мухамед iбн-Муса ал-Харэзмі напісаў кнігу «Аб індыйскім лічэнні». Падручнік утрымліваў рашэнні практычных задач «рознага роду і сорту» і быў першай кнігай, напісанай з выкарыстаннем пазіцыйнай сістэмы злічэння, да гэтага лічбамі карысталіся толькі для вылічэнняў на лічыльнай дошцы[82][83]. У XII стагоддзі Адэлардам і Іаанам Севельскім было зроблена два пераклады кнігі на лацінскую мову[84]. Яе арыгінал не захаваўся, але ў 1857 годзе пад назвай «Алхарэзмі аб індыйскім ліку» быў выдадзены знойдзены лацінскі пераклад[82]. У трактаце апісваецца выкананне з дапамогай індыйскіх лічбаў на лічыльнай дошцы такіх арыфметычных дзеянняў, як складанне, адніманне, падваенне, множанне, раздваенне, дзяленне і здабыванне квадратнага кораня[85]. Множанне дробаў, як і дзяленне, разглядалася з дапамогай прапорцый: памножыць на было раўназначна пошуку такога , што . Гэтая тэорыя была асновай арабскай арыфметыкі. Аднак пры гэтым існавала і іншае злічэнне дробаў, якое прадстаўляла любы дроб у выглядзе сумы аліквотных дробаў[86]. Для рашэння задач арабы карысталіся трайным правілам, якое прыйшло з Індыі і было апісана разам з шэрагам іншых прыёмаў у «Кнізе аб індыйскіх рашыках» аль-Біруні, правілам двух ілжывых палажэнняў, якое прыйшло з Кітая і атрымала тэарэтычнае абгрунтаванне ў «кнізе аб правіле двайнога ілжывага палажэння» Кусты ібн Луккі[87].
Праз Іспанію і Сіцылію ў X стагоддзі пачалі завязвацца навуковыя сувязі Еўропы з арабскім светам. У гэты час Каталонію наведаў вучоны манах Герберт, які стаў пазней папам Сільвестрам II. Яму прыпісваюць такія сачыненні, як «Кніжка аб дзяленні лікаў» і «Правілы лічэння на абаку». У абедзвюх кнігах лікі напісаныя словамі ці рымскімі лічбамі[88]. Герберт называў вылічальнікаў на абаку «абацыстамі». У XII—XIII стагоддзях у Еўропе з'явіліся лацінскія пераклады арабскіх кніг па арыфметыцы. Прыхільнікі прадстаўленай у кнігах дзесятковай пазіцыйнай нумарацыі сталі называцца «алгарыстамі» па імені арабскага матэматыка ал-Харэзмі ў лацінскай форме[89]. У пачатку XIII стагоддзя ў Заходняй Еўропе існавала дзве сістэмы злічэння: старая, заснаваная на абаку, якую падтрымліваў Герберт, і новая, пазіцыйная індыйская сістэма, якую падтрымліваў Леанарда Фібаначы. Паступова новая сістэма ўзяла верх[84][90]. Асноўнай яе перавагай з'яўляецца спрашчэнне арыфметычных аперацый. Разам з тым у Германіі, Францыі і Англіі новыя лічбы не ўжываліся да канца XV стагоддзя. Выцясненне старой нумарацыі адбылося толькі ў XVI—XVII стагоддзях[90].
У 1427 годзе ал-Кашы апісаў сістэму дзесятковых дробаў, якая пачала паўсюдна ўжывацца пасля твораў Стевіна ў 1585 годзе[5]. Стэвін хацеў як мага шырэй распаўсюдзіць дзесятковую сістэму. Іменна таму ён напісаў свае сачыненні на французскай і фламандскай мовах, а не на латыні. Акрамя таго, ён стаў энергічна змагацца за ўвядзенне дзесятковай сістэмы мер[36].
Арыфметыка Новага часу[правіць | правіць зыходнік]

У XVII стагоддзі мараходная астраномія, механіка, больш складаныя камерцыйныя разлікі паставілі перад арыфметыкай новыя запыты да тэхнікі вылічэнняў і далі штуршок к далейшаму развіццю. Значна змянілася паняцце ліку. Калі раней да вобласці лікаў у большасці сваёй адносілі толькі дадатныя рацыянальныя лікі, то пачынаючы з XVI стагоддзя ўсё больш прызнаваліся ірацыянальныя і адмоўныя лікі. Ньютан ў сваіх лекцыях дзеліць лікі на тры віды: цэлыя (вымяраюцца адзінкай), дробавыя (кратныя долі адзінкі) і ірацыянальныя (несувымерныя з адзінкай). З 1710 такое вызначэнне ліку трывала ўваходзіць ва ўсе падручнікі[91].
У пачатку XVII стагоддзя Непер вынайшаў лагарыфмы. Прымяненне лагарыфмаў і дзесятковых дробаў, уключэнне ў арыфметыку паняцця ірацыянальнага ліку, як паслядоўнасці рацыянальных прыбліжэнняў, пашырылі вобласць ужывання арыфметыкі к канцу XVII стагоддзя і вызначылі фундаментальнае значэнне навукі для вывучэння непарыўных велічынь[5].
З працамі Лабачэўскага па геаметрыі звязаны працэс крытычнага перагляду асноў матэматыкі, які здарыўся ў XIX стагоддзі. Яшчэ ў XVIII стагоддзі пачаліся спробы тэарэтычнага абгрунтавання уяўленняў аб ліку. Лейбніц першы паставіў задачу дэдуктыўнай пабудовы арыфметыкі і, сярод іншага, паказаў неабходнасць доказу роўнасці «два плюс два роўна чатыры» у сваіх «Новых вопытах аб чалавечым розуме» ў 1705 годзе. У спробах вырашыць гэтае пытанне свае аксіёмы прадставілі Вольф ў 1770 годзе, Шульц ў 1790 годзе, Ом ў 1822 годзе, Грасман ў 1861 годзе і, нарэшце, Пеана ў 1889 годзе[92].
У 1758 годзе у «Першых асновах арыфметыкі, геаметрыі, плоскай і сферычнай трыганаметрыі і перспектывы» Кестнер выступіў за абгрунтаванне ўсіх арыфметычных паняццяў цераз цэлы лік. Такім чынам ён вызначыў, па парадку ў яго кнізе, натуральныя лікі, дробы, адмоўныя лікі, дзесятковыя дробы, ірацыянальныя лікі і толькі затым тэорыю адносін[93]. У фарміраванні тэорыі адмоўных лікаў асноўную праблему складала сцвярджэнне, што адмоўны лік менш за нуль, г.зн. менш, чым нічога[94].
Поўнае геаметрычнае тлумачэнне камплексных лікаў было прапанавана Каспарам Веселем у «Вопыце аб аналітычным прадстаўленні напрамку і яго ужываннях, пераважна да рашэння плоскіх і сферычных многавугольнікаў» у 1799 годзе. Весель спрабаваў абагульніць тэорыю на трохмерную прастору, але гэта яму не ўдалося. Пытанне заставалася адкрытым да таго часу, пакуль Гамільтан не пабудаваў тэорыю кватэрніёнаў, пры памнажэнні якіх не выконваецца перамяшчальны закон. Далейшыя даследаванні Веерштраса, Фрабеніуса і Пірса паказалі, што адмовіцца ад якога-небудзь з арыфметычных законаў прыйдзецца пры любым пашырэнні паняцця ліку за межы камплексных лікаў[95].
Арыфметыка ў адукацыі[правіць | правіць зыходнік]
Утварэнне арыфметычных паняццяў цесна звязана з працэсам лічэння. У яго аснове ляжаць такія элементы разумовай дзейнасці, як уменне пазнаваць прадмет; адрозніваць прадметы; падзяляць сукупнасць прадметаў на элементы, раўнапраўныя пры лічэнні (іншымі словамі, карыстацца адзінкай лічэння); уменне размяшчаць элементы паслядоўна, парадкаваць іх, што прыводзіць да лічэння розных па якасці прадметаў і ўтварэння паняцця ліку. Падобныя працэсы можна назіраць пры засваенні паняццяў дзецьмі[5].
Дык вось, якую ж з дысцыплін трэба вывучаць першай, калі не тую, што з'яўляецца пачаткам і выконвае як бы ролю маці ў адносінах да іншых [дысцыплін]? Такая як раз арыфметыка. Яна папярэднічае ўсім іншым не толькі таму, што сам Бог, творца гэтага сусвету, узяў яе першай за ўзор свайго мыслення і па яе [прынцыпе] зрабіў усё, што цераз лікі сілай творчага Розуму здабыла гармонію ва ўстаноўленым парадку, але і таму арыфметыка аб'яўляецца папярэдняй, што калі выключыць папярэднія па сваёй прыродзе сутнасці, адразу ж знікаюць і наступныя. Калі гінуць наступныя, то нічога ў статусе папярэдняй субстанцыі не мяняецца.
Стандарты пачатковай адукацыі мяркуюць навыкі лічэння і параўнання лікаў да мільёна, работу з асноўнымі адзінкамі вымярэння і суадносінамі паміж імі, выкананне чатырох асноўных арыфметычных аперацый (вусна да 100 і пісьмова да 10 000), а таксама дзялення з астачай, пошук значэння лікавага выразу, які складаецца з некалькіх арыфметычных дзеянняў[97][98]. Школьны матэрыял падаецца з дапамогай наглядных уяўленняў. У першым класе дзеці маюць справу з лікавымі вобразамі і колькасцямі прадметаў, лічэнне ідзе да 20. У другім класе ўводзяць дзесятковую сістэму, пазіцыйную сістэму, табліцу множання, лічэнне ідзе да 100. У трэцім класе вывучаюць арыфметычныя дзеянні з мнагазначнымі лікамі. Наступным крокам ідзе пераход да літарных абазначэнняў, іншымі словамі — ад канкрэтнага да абстрактнага. Іменна з гэтага, на думку Клейна, і пачынаецца матэматыка[99]. Цяжкасць вывучэння арыфметыкі ў пачатковай школе заключаецца ў тым, што неабходна ажыццяўляць лічэнне адцягнена ад прыроды прадметаў[100].
Навучанне ў сярэдняй школе звязана з пашырэннем паняцця ліку, уводзяць дробы і дзеянні над імі, адмоўныя лікі, ірацыянальныя лікі[101].
У сучасным свеце матэматычная граматнасць з'яўляецца адной з асноўных мэт адукацыі. Яна ўключае ў сябе, сярод іншага, уменне здзяйсняць арыфметычныя дзеянні, праводзіць падлікі і вымярэнні[102]. Пытаннямі матэматычнай граматнасці дзяцей і дарослых займаюцца такія арганізацыі, як ЮНІСЕФ і ЮНЕСКА[103][104].
Разам з тым доўгі час навучанне арыфметычным дзеянням зводзілася да механічнага выкананню узораў. У Старажытным Кітаі вялікая ўвага надавалася навучанню матэматыцы, уключаючы здачу экзаменаў. У Імператарскай акадэміі матэматыка вывучалася сем гадоў. Аднак класічныя матэматычныя трактаты разглядаліся як догма і перавыдаваліся без змен[105].
У Еўропе сістэматычныя практыкаванні на складанне, адніманне, множанне і дзяленне былі прапанаваны Тарталья ў XVI стагоддзі, але яны яшчэ доўгі час не ўваходзілі ва ўжытак[106]. Акрамя таго, у Сярэднія вякі існавалі правілы для рашэння вялікага ліку асобных арыфметычных задач. У некаторых падручніках сустракаецца да 26 такіх правіл, пры гэтым яны могуць не супадаць у розных падручніках[107]. Некаторыя правілы не страцілі сваёй актуальнасці да гэтага часу. Да іх адносяцца прапорцыі (дробы разглядаліся як адносіны двух лікаў, што прыводзіла да разгляду прапорцый для здзяйснення аперацый), працэнты[108].
Арыфметыка з'яўляецца чацвёртым з сямі вольных мастацтваў па ўзроўні навучання. Ёй папярэднічае Трывіум, які складаецца з Граматыкі, Рыторыкі і Дыялектыкі, а сама яна з'яўляецца старэйшай навукай у квадрывіуме, да якога таксама адносяцца Геаметрыя, Музыка і Астраномія[109]. Са з'яўленнем першых еўрапейскіх універсітэтаў матэматыка выкладалася на факультэтах мастацтва як квадрывіум і была дапаможнай дысцыплінай. Першыя лекцыі па арыфметыцы былі прачытаны магістрам Венскага ўніверсітэта Іаганам з Гмундэна ў 1412 годзе[110].
Арыфметыка ў філасофіі і мастацтве[правіць | правіць зыходнік]

Пасля таго як піфагарэйцы выкарыстоўвалі адносіны цэлых лікаў для выражэння геаметрычных адносін адрэзкаў, а таксама аналагічных адносін у гармоніі і музыцы, яны прыйшлі да вываду, што ўсе заканамернасці свету можна апісаць з дапамогай лікаў, а арыфметыка патрэбна для таго, каб выразіць адносіны і пабудаваць мадэль свету[111]. Разам з тым адным з адкрыццяў піфагарэйцаў з'яўляецца тое, што адносін цэлых лікаў недастаткова для выражэння адносін любых адрэзкаў (дыяганаль і старана квадрата несувымерныя), і на гэтай аснове немагчыма будаваць метрычную геаметрыю[72]. Праблемы пабудовы канечнай меры і вызначэння сапраўднага ліку агалілі навуковы крызіс у V стагоддзі да н. э., выхадам з якога займаліся ўсе філасофскія школы Старажытнай Грэцыі. Паказаць усе цяжкасці, якія ўзнікаюць пры вырашэнні гэтых праблем, удалося Зянону Элейскаму ў яго парадоксах, або апорыях[112].
Марцыян Капэла ў сваім трактаце «Вяселле Філасофіі і Меркурыя» стварыў візуальныя вобразы ўсіх сямі мастацтваў і ў тым ліку Арыфметыкі. Мастацтвы ўвасаблялі жанчыны з адпаведнымі атрыбутамі, якія суправаджаліся вядомымі прадстаўнікамі сферы. Арыфметыка трымае ў сваіх руках скрыжаль, спісаную лічбамі, або абак. Яе суправаджае Піфагор[113].
Лічэнне было адным з выпрабаванняў Буды. Пасля спаборніцтваў у стральбе з лука, бегу і плаванні матэматык Ар'юна загадаў яму назваць усе лікавыя ступені больш за . Буда назваў дваццаць дзве ступені да (толькі няцотныя ступені мелі назвы), і гэта быў толькі першае лічэнне, у другім лічэнні Буда працягнуў да . Наступным заданнем Буда палічыў лік атамаў у мілі, а затым і ў Сусвеце[114]. Падобныя «лікавыя лесвіцы» сустракаюцца неаднаразова ў індыйскай рэлігійнай паэзіі, пры гэтым словы для абазначэння лікаў могуць адрознівацца. Прызначэнне такіх лесвіц — падняцца над светам смяротных. У індыйскай кнізе «Лілавацістара» апісваюцца спаборніцтвы паміж жаніхамі гаспадарыні зямлі, прыгожай Гопы, у пісьменства, арыфметыцы, барацьбе і мастацтве кідання стрэл. Выпрабаванням у арыфметыцы прысвечана значная частка твора[115].
Як і ў Індыі, вельмі вялікія лікі, сканструяваныя штучна жрацамі мая, гавораць аб імкненні забрацца вышэй па «лікавай лесвіцы», бліжэй да багоў[116].
Зноскі[правіць | правіць зыходнік]
- Каментарыі
- ↑ Няхай трэба знайсці корань з , — першае прыбліжэнне з недастачай, — прыбліжэнне з лішкам. Другое прыбліжэнне ўтвараецца па формуле сярэдняга арыфметычнага , і яму адпавядае , і так далей)[67].
- Выкарыстаная літаратура і крыніцы
- ↑ а б в г д е ё ж з Виноградов И. М. Арифметика // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 1.
- ↑ а б в г Виноградов И. М. Арифметика формальная // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 1.
- ↑ а б в г д е ё Арифметика, наука // Энциклопедический словарь Брокгауза и Ефрона: В 86 томах (82 т. и 4 доп.) (руск.). — СПб., 1890—1907.
- ↑ а б в г д е ё ж з MacDuffee C. C.. Arithmetic. Encyclopædia Britannica. Архівавана з першакрыніцы 27 мая 2012. Праверана 20 сакавіка 2012. (англ.)
- ↑ а б в г д е ё ж з і к л Арифметика. Большая советская энциклопедия. Архівавана з першакрыніцы 3 лістапада 2012. Праверана 20 студзеня 2013.
- ↑ Арнольд 1938, с. 3—5.
- ↑ Понтрягин 1986, с. 4—6.
- ↑ Беллюстин В. Глава 12. Число и порядок действий, знаки и определения // Как постепенно дошли люди до настоящей арифметики. — М.: Типография К. Л. Меньшова, 1909.
- ↑ Депман 1965, с. 195—199.
- ↑ Арнольд 1938, с. 151—156.
- ↑ Алгебра. Большая советская энциклопедия. Архівавана з першакрыніцы 1 лютага 2013. Праверана 20 студзеня 2013.
- ↑ Депман 1965, с. 21—25.
- ↑ Депман 1965, с. 129—130.
- ↑ а б в История математики, т. I 1970, с. 23—24.
- ↑ а б в г Депман 1965, с. 212—232.
- ↑ а б в Депман 1965, с. 204.
- ↑ Арифметика 1951, с. 142.
- ↑ Клейн 1987, с. 23—26.
- ↑ а б в г Клейн 1987, с. 26—35.
- ↑ Арифметика 1951, с. 77—79.
- ↑ Клейн 1987, с. 37—44.
- ↑ Арифметика 1951, с. 157.
- ↑ Клейн 1987.
- ↑ а б в Арифметика 1951, с. 172—178.
- ↑ Арифметика 1951, с. 188—201.
- ↑ Арифметика 1951, с. 227.
- ↑ Клейн 1987, с. 35—36.
- ↑ а б Клейн 1987, с. 23—25.
- ↑ Арифметика. Энциклопедия Кольера. Архівавана з першакрыніцы 1 лютага 2013. Праверана 20 студзеня 2013.
- ↑ а б Кнут, с. 216.
- ↑ История математики, т. II 1970, с. 66—67.
- ↑ История математики, т. III 1972, с. 42—45.
- ↑ Клейн 1987, с. 45—49.
- ↑ Депман 1965, с. 263—267.
- ↑ Boyer & Merzbach 2010, Arithmetic and logistic.
- ↑ а б Арифметика 1951, с. 57—71.
- ↑ Кнут, с. 216, 221.
- ↑ Депман 1965, с. 275—285.
- ↑ Клейн 1987, с. 49—57.
- ↑ а б в Виноградов И. М. Чисел теория // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 5.
- ↑ Виноградов И. М. Элементарная теория чисел // Математическая энциклопедия. — М.: Советская энциклопедия, 1977. — Т. 5.
- ↑ Арнольд 1938, с. 413—415.
- ↑ а б в Аксиоматический метод. Большая советская энциклопедия. Архівавана з першакрыніцы 10 лютага 2013. Праверана 20 студзеня 2013.
- ↑ Арифметика 1951, с. 100—107.
- ↑ а б в Депман 1965, с. 117—126.
- ↑ а б Арифметика 1951, с. 135—138.
- ↑ а б Арифметика 1951, с. 139—142.
- ↑ Арифметика 1951, с. 133.
- ↑ а б в г Арифметика 1951, с. 150—151.
- ↑ а б Арифметика 1951, с. 172—179.
- ↑ а б Арифметика 1951, с. 160—167.
- ↑ Депман 1965, с. 258—262.
- ↑ Арифметика 1951, с. 188.
- ↑ а б Арифметика 1951, с. 202.
- ↑ Арифметика 1951, с. 228.
- ↑ а б в г д Формальная арифметика. Большая советская энциклопедия. Архівавана з першакрыніцы 3 лістапада 2012. Праверана 20 студзеня 2013.
- ↑ Avigad 2003, p. 260.
- ↑ Нечаев 1975, с. 52—53.
- ↑ Нечаев 1975, с. 48.
- ↑ Нечаев 1975, с. 68—72.
- ↑ История математики, т. I 1970, с. 19—20.
- ↑ а б Депман 1965, с. 49—52.
- ↑ История математики, т. I 1970, с. 25.
- ↑ История математики, т. I 1970, с. 34.
- ↑ История математики, т. I 1970, с. 40.
- ↑ История математики, т. I 1970, с. 50.
- ↑ История математики, т. I 1970, с. 46—47.
- ↑ Депман 1965, с. 53—54.
- ↑ История математики, т. I 1970, с. 62.
- ↑ История математики, т. I 1970, с. 68—69.
- ↑ а б История математики, т. I 1970, с. 74—76.
- ↑ а б История математики, т. I 1970, с. 73.
- ↑ История математики, т. I 1970, с. 144—146.
- ↑ Депман 1965, с. 57—58.
- ↑ История математики, т. I 1970, с. 178.
- ↑ История математики, т. I 1970, с. 160—161.
- ↑ История математики, т. I 1970, с. 163—164.
- ↑ История математики, т. I 1970, с. 167—169.
- ↑ История математики, т. I 1970, с. 183—185.
- ↑ История математики, т. I 1970, с. 185.
- ↑ История математики, т. I 1970, с. 190—191.
- ↑ а б Депман 1965, с. 72—78.
- ↑ История математики, т. I 1970, с. 209—210.
- ↑ а б Депман 1965, с. 90—94.
- ↑ История математики, т. I 1970, с. 211—212.
- ↑ История математики, т. I 1970, с. 212—214.
- ↑ История математики, т. I 1970, с. 218—219.
- ↑ История математики, т. I 1970, с. 254—256.
- ↑ История математики, т. I 1970, с. 256—257.
- ↑ а б Арифметика 1951, с. 50—57.
- ↑ История математики, т. II 1970, с. 34—36.
- ↑ История математики, т. III 1972, с. 47—49.
- ↑ История математики, т. III 1972, с. 49—52.
- ↑ История математики, т. III 1972, с. 52—56.
- ↑ История математики, т. III 1972, с. 61—66.
- ↑ Боэций. I, 1 // Основы арифметики.
- ↑ Примерная основная образовательная программа образовательного учреждения. Начальная школа(недаступная спасылка). Федеральный государственный образовательный стандарт. Архівавана з першакрыніцы 7 снежня 2012. Праверана 5 снежня 2012.
- ↑ Примерная основная образовательная программа образовательного учреждения. Начальная школа / сост. Е. С. Савинов. — 4-е. — М.: Просвещение, 2013. — С. 32—35. — 223 с. — ISBN 9785090264167. Архівавана 24 жніўня 2013.
- ↑ Клейн 1987, с. 20—23.
- ↑ Депман 1965, с. 1—3, 103—109.
- ↑ Клейн 1987, с. 37.
- ↑ Грамотность, математические способности и навыки решения задач в технологически развитом обществе(недаступная спасылка). Национальный исследовательский университет Высшая школа экономики. Архівавана з першакрыніцы 7 снежня 2012. Праверана 5 снежня 2012.
- ↑ Defining Quality in Education (англ.)(недаступная спасылка). ЮНІСЕФ. Архівавана з першакрыніцы 15 кастрычніка 2012. Праверана 5 снежня 2012.
- ↑ Education for All Goals (англ.). ЮНЕСКА. Архівавана з першакрыніцы 7 снежня 2012. Праверана 5 снежня 2012.
- ↑ История математики, т. I 1970, с. 157.
- ↑ Депман 1965, с. 199—203.
- ↑ Депман 1965, с. 305.
- ↑ Депман 1965, с. 306.
- ↑ Liberal Arts. Encyclopædia Britannica. Архівавана з першакрыніцы 27 мая 2012. Праверана 20 сакавіка 2012. (англ.)
- ↑ История математики, т. I 1970, с. 259—260.
- ↑ История математики, т. I 1970, с. 67.
- ↑ История математики, т. I 1970, с. 88—89.
- ↑ Семь свободных искусств(недаступная спасылка). Simbolarium. Архівавана з першакрыніцы 27 мая 2012. Праверана 20 сакавіка 2012.
- ↑ Меннингер 2011, с. 176—179.
- ↑ Арифметика 1951, с. 49.
- ↑ Меннингер 2011, с. 82.
Літаратура[правіць | правіць зыходнік]
| Арыфметыка на Вікісховішчы |
- Арнольд И. В. Теоретическая арифметика. — М.: Государственное учебно-педагогическое издательство, 1938. — 481 с.
- Депман И. Я. История арифметики. — М.: Просвещение, 1965. — 400 с. Архівавана 14 мая 2017.
- Клейн Ф. Элементарная математика с точки зрения высшей. — М.: Наука, 1987. — Т. I: Арифметика. Алгебра. Анализ. — 432 с.
- Кнут Д. Э. Арифметика // Искусство программирования. — М. — Т. II. — 830 с.
- Меннингер К. История цифр. Числа, символы, слова. — М.: ЗАО Центрполиграф, 2011. — 543 с. — ISBN 9785952449787.
- Нечаев В. И. Числовые системы. — М.: Просвещение, 1975. — 199 с.
- Понтрягин Л. С. Обобщения чисел. — М.: Наука, 1986. — (Библиотечка «Квант»). Архівавана 18 верасня 2011.
- Серр Ж.-П. Курс арифметики / пер. с франц. А. И. Скопина под ред. А. В. Малышева. — М.: Мир, 1972. — 184 с.
- История математики: в 3 т. / под ред. А. П. Юшкевича. — М.: Наука, 1970. — Т. I: С древнейших времён до начала Нового времени.
- История математики: в 3 т. / под ред. А. П. Юшкевича. — М.: Наука, 1970. — Т. II: Математика XVII столетия.
- История математики: в 3 т. / под ред. А. П. Юшкевича. — М.: Наука, 1972. — Т. III: Математика XVIII столетия.
- Энциклопедия элементарной математики. Книга первая. Арифметика / под ред. П. С. Александрова, А. И. Маркушевича и А. Я. Хинчина. — М.—Л.: Гос. издат. технико-теоретической литературы, 1951. — 448 с. Архівавана 2 сакавіка 2015.
- Avigad, Jeremy. Number theory and elementary arithmetic // Philosophia Mathematica. — 2003. — Vol. 11. — № 3. — P. 257—284. (англ.)
- Boyer C. B., Merzbach U. C. A History of Mathematics. — John Wiley & Sons, 2010. — 640 p. (англ.)
- Дадатковая літаратура
- Cunnington, Susan, The Story of Arithmetic: A Short History of Its Origin and Development, Swan Sonnenschein, London, 1904
- Dickson, Leonard Eugene, History of the Theory of Numbers (3 volumes), reprints: Carnegie Institute of Washington, Washington, 1932; Chelsea, New York, 1952, 1966
- Euler, Leonhard, Elements of Algebra Архівавана 13 красавіка 2011., Tarquin Press, 2007
- Fine, Henry Burchard (1858—1928), The Number System of Algebra Treated Theoretically and Historically, Leach, Shewell & Sanborn, Boston, 1891
- Karpinski, Louis Charles (1878—1956), The History of Arithmetic, Rand McNally, Chicago, 1925; reprint: Russell & Russell, New York, 1965
- Ore, Øystein, Number Theory and Its History, McGraw—Hill, New York, 1948
- Weil, André, Number Theory: An Approach through History, Birkhauser, Boston, 1984.
Гэты артыкул уваходзіць у лік добрых артыкулаў беларускамоўнага раздзела Вікіпедыі. |











![{\displaystyle \scriptstyle {\sqrt[{\text{паказчык}}]{\scriptstyle {\text{падкаранёвы выраз}}}}\,=\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c32f318a7a54a6b0726409a345eb29cee68b1bf)




























![{\displaystyle a^{n \over m}={\sqrt[{m}]{a^{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eeefec081d9b62beaa1518fc9e1707ad7ca9377a)












































































